
【題目】已知點![]() 分別在菱形
分別在菱形![]() 的邊
的邊![]() 上滑動(點
上滑動(點![]() 不與
不與![]() 重合),且
重合),且![]() .
.
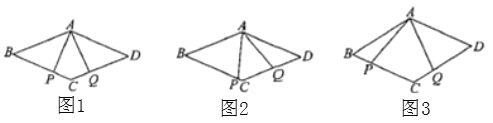
(1)如圖1,若![]() ,求證:
,求證:![]() ;
;
(2)如圖2,若![]() 與
與![]() 不垂直,(1)中的結論還成立嗎?若成立,請證明,若不成立,說明理由;
不垂直,(1)中的結論還成立嗎?若成立,請證明,若不成立,說明理由;
(3)如圖3,若![]() ,請直接寫出四邊形
,請直接寫出四邊形![]() 的面積.
的面積.
【答案】(1)證明見解析;(2)(1)中的結論還成立,證明見解析;(3)四邊形![]() 的面積為
的面積為![]() .
.
【解析】
(1)根據菱形的性質及已知,得到![]() ,再證
,再證![]() ,
,
根據三角形全等的性質即可得到結論;
(2)作![]() ,垂足分別為點
,垂足分別為點![]() ,證明
,證明![]() ,根據三角形全等的性質即可得到結論;
,根據三角形全等的性質即可得到結論;
(3)根據菱形的面積公式,結合(2)的結論解答.
解:(1)∵四邊形![]() 是菱形,
是菱形,
∴![]() ,
,![]() .
.
∵![]() ,∴
,∴![]() ,
,
∴![]() .
.
∵![]() ,∴
,∴![]() ,∴
,∴![]() .
.
在![]() 和
和![]() 中,
中,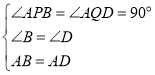 ,
,
∴![]() ,
,
∴![]() .
.
(2)若![]() 與
與![]() 不垂直,(1)中的結論還成立證明如下:
不垂直,(1)中的結論還成立證明如下:
如圖,作![]() ,垂足分別為點
,垂足分別為點![]() .
.
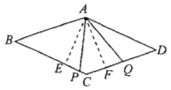
由(1)可得![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,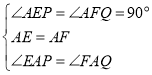 ,
,
∴![]() ,∴
,∴![]() .
.
(3)如圖,連接![]() 交于點
交于點![]() .
.
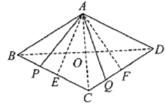
∵![]() ,∴
,∴![]() 為等邊三角形,
為等邊三角形,
∵![]() ,∴
,∴![]() ,同理,
,同理,![]() ,
,
∴四邊形![]() 的面積
的面積![]() 四邊形
四邊形![]() 的面積,
的面積,
由(2)得四邊形![]() 的面積
的面積![]() 四邊形AECF的面積
四邊形AECF的面積
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴四邊形![]() 的面積為
的面積為![]() ,
,
∴四邊形![]() 的面積為
的面積為![]() .
.


科目:初中數學 來源: 題型:
【題目】某商家計劃從廠家采購空調和冰箱兩種產品共![]() 臺,空調和冰箱的采購單價與銷售單價如表所示:
臺,空調和冰箱的采購單價與銷售單價如表所示:
采購單價 | 銷售單價 | |
空調 |
|
|
冰箱 |
|
|
![]() 若采購空調
若采購空調![]() 臺,且所采購的空調和冰箱全部售完,求商家的利潤;
臺,且所采購的空調和冰箱全部售完,求商家的利潤;
![]() 廠家有規定,采購空調的數量不少于
廠家有規定,采購空調的數量不少于![]() 臺,且空調采購單價不低于
臺,且空調采購單價不低于![]() 元,問商家采購空調多少臺時總利潤最大?并求最大利潤.
元,問商家采購空調多少臺時總利潤最大?并求最大利潤.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在等腰三角形![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 邊的中點,點
邊的中點,點![]() 在線段
在線段![]() 上從
上從![]() 向
向![]() 運動,同時點
運動,同時點![]() 在線段
在線段![]() 上從點
上從點![]() 向
向![]() 運動,速度都是1個單位/秒,時間是
運動,速度都是1個單位/秒,時間是![]() (
(![]() ),連接
),連接![]() 、
、![]() 、
、![]() .
.

(1)請判斷![]() 形狀,并證明你的結論.
形狀,并證明你的結論.
(2)以![]() 、
、![]() 、
、![]() 、
、![]() 四點組成的四邊形面積是否發生變化?若不變,求出這個值:若變化,用含
四點組成的四邊形面積是否發生變化?若不變,求出這個值:若變化,用含![]() 的式子表示.
的式子表示.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖![]() ,一條筆直的公路上有
,一條筆直的公路上有![]() 、
、![]() 、
、![]() 三地
三地![]() 、
、![]() 兩地相距
兩地相距![]() 千米,甲、乙兩個野外徒步愛好小組從
千米,甲、乙兩個野外徒步愛好小組從 ![]() 、
、![]() 兩地同時出發,沿公路始終勻速相向而行,分別走向
兩地同時出發,沿公路始終勻速相向而行,分別走向![]() 、
、![]() 兩地.甲、乙兩組到
兩地.甲、乙兩組到![]() 地的距離
地的距離![]() ,
,![]() (千米)與行走時間
(千米)與行走時間![]() (時)的關系如圖
(時)的關系如圖![]() 所示.
所示.
(1)請在圖![]() 中標出
中標出![]() 地的位置,并寫出相應的距離:
地的位置,并寫出相應的距離:![]()
![]() ;
;
(2)在圖![]() 中求出甲組到達
中求出甲組到達![]() 地的時間
地的時間![]() ;
;
(3)求岀乙組從![]() 地到
地到![]() 地行走過程中
地行走過程中![]() 與行走時間
與行走時間![]() 的關系式.
的關系式.
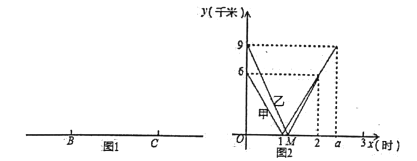
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1:在四邊形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E、F分別是BC、CD上的點.且∠EAF=60°.探究圖中線段BE、EF、FD之間的數量關系.
小王同學探究此問題的方法是,延長FD到點G,使DG=BE.連結AG,先證明△ABE≌△ADG,再證明△AEF≌△AGF,可得出結論,他的結論應是 ;

探索延伸:
如圖2,若在四邊形ABCD中,AB=AD,∠B+∠D=180°.E、F分別是BC、CD上的點,且∠EAF=![]() ∠BAD,上述結論是否仍然成立,并說明理由;
∠BAD,上述結論是否仍然成立,并說明理由;
實際應用:
如圖3,在某次軍事演習中,艦艇甲在指揮中心(O處)北偏西30°的A處,艦艇乙在指揮中心南偏東70°的B處,并且兩艦艇到指揮中心的距離相等,接到行動指令后,艦艇甲向正東方向以60海里/小時的速度前進,艦艇乙沿北偏東50°的方向以80海里/小時的速度前進1.5小時后,指揮中心觀測到甲、乙兩艦艇分別到達E,F處,且兩艦艇之間的夾角為70°,試求此時兩艦艇之間的距離?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場在11月中旬對甲、乙、丙三種型號的電視機進行促銷.其中,甲型號電視機直接按成本價1280元的基礎上獲利![]() 定價;乙型號電視機在原銷售價2199元的基礎上先讓利199元,再按八五折優惠;丙型號電視機直接在原銷售價2399元上減499元;活動結束后,三種型號電視機總銷售額為20600元,若在此次促銷活動中,甲、乙、丙三種型號的電視機至少賣出其中兩種型號,則三種型號的電視機共______有種銷售方案.
定價;乙型號電視機在原銷售價2199元的基礎上先讓利199元,再按八五折優惠;丙型號電視機直接在原銷售價2399元上減499元;活動結束后,三種型號電視機總銷售額為20600元,若在此次促銷活動中,甲、乙、丙三種型號的電視機至少賣出其中兩種型號,則三種型號的電視機共______有種銷售方案.
查看答案和解析>>
科目:初中數學 來源: 題型:
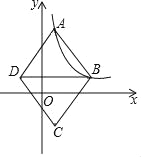
【題目】如圖,在平面直角坐標系中,菱形ABCD的頂點A、B在反比例函數y=![]() (k>0,x>0)的圖象上,橫坐標分別為1,4,對角線BD∥x軸.若菱形ABCD的面積為
(k>0,x>0)的圖象上,橫坐標分別為1,4,對角線BD∥x軸.若菱形ABCD的面積為![]() ,則k的值為_____.
,則k的值為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
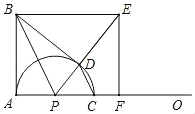
【題目】如圖,∠BAO=90°,AB=8,動點P在射線AO上,以PA為半徑的半圓P交射線AO于另一點C,CD∥BP交半圓P于另一點D,BE∥AO交射線PD于點E,EF⊥AO于點F,連接BD,設AP=m.
(1)求證:∠BDP=90°.
(2)若m=4,求BE的長.
(3)在點P的整個運動過程中.
①當AF=3CF時,求出所有符合條件的m的值.
②當tan∠DBE=![]() 時,直接寫出△CDP與△BDP面積比.
時,直接寫出△CDP與△BDP面積比.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com