
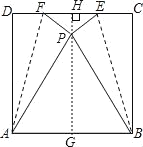
【題目】如圖,將正方形ABCD折疊,使點C與點D重合于正方形內點P處,折痕分別為AF、BE,如果正方形ABCD的邊長是2,那么△EPF的面積是_____.

【答案】![]()
【解析】
過P作PH⊥DC于H,交AB于G,由正方形的性質得到AD=AB=BC=DC=2;∠D=∠C=90°;再根據折疊的性質有PA=PB=2,∠FPA=∠EPB=90°,可判斷△PAB為等邊三角形,利用等邊三角形的性質得到∠APB=60°,![]() ,于是∠EPF=120°,PH=HG﹣PG=2﹣
,于是∠EPF=120°,PH=HG﹣PG=2﹣![]() ,得∠HEP=30°,然后根據含30°的直角三角形三邊可求出HE,得到EF,最后利用三角形的面積公式計算即可.
,得∠HEP=30°,然后根據含30°的直角三角形三邊可求出HE,得到EF,最后利用三角形的面積公式計算即可.
解:過P作PH⊥DC于H,交AB于G,如圖,
則PG⊥AB,
∵四邊形ABCD為正方形,
∴AD=AB=BC=DC=2;∠D=∠C=90°,
又∵將正方形ABCD折疊,使點C與點D重合于形內點P處,
∴PA=PB=2,∠FPA=∠EPB=90°,
∴△PAB為等邊三角形,
∴∠APB=60°,PG=![]() AB=
AB=![]() ,
,
∴∠EPF=120°,PH=HG﹣PG=2﹣![]() ,
,
∴∠HEP=30°,
∴HE=![]() PH=
PH=![]() (2﹣
(2﹣![]() )=2
)=2![]() ﹣3,
﹣3,
∴EF=2HE=4![]() ﹣6,
﹣6,
∴△EPF的面積=![]() FEPH=
FEPH=![]() (2﹣
(2﹣![]() )(4
)(4![]() ﹣6)
﹣6)
=7![]() ﹣12.
﹣12.
故答案為7![]() ﹣12.
﹣12.


科目:初中數學 來源: 題型:
【題目】對于任意四個有理數a,b,c,d,可以組成兩個有理數對(a,b)與(c,d).我們規定:
(a,b)★(c,d)=bc-ad.
例如:(1,2)★(3,4)=2×3-1×4=2.
根據上述規定解決下列問題:
(1)有理數對(2,-3)★(3,-2)=_______;
(2)若有理數對(-3,2x-1)★(1,x+1)=7,則x=_______;
(3)當滿足等式(-3,2x-1)★(k,x+k)=5+2k的x是整數時,求整數k的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】 “囧”(jiong)是近時期網絡流行語,像一個人臉郁悶的神情.如圖所示,一張邊長為20的正方形的紙片,剪去兩個一樣的小直角三角形和一個長方形得到一個“囧”字圖案(陰影部分).設剪去的小長方形長和寬分別為x、y,剪去的兩個小直角三角形的兩直角邊長也分別為x、y.
(1)用含有x、y的代數式表示右圖中“囧”的面積;
(2)當![]() 時,求此時“囧”的面積.
時,求此時“囧”的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在Rt△ABC中,AB=BC=5,∠B=90°,將一塊等腰直角三角板的直角頂點O放在斜邊AC上,三角板的兩直角邊分別交直線AB、BC于E、F兩點.
(1)如圖①,若O為AC的中點,點E、F分別在邊AB、BC上.
①當△OFC是等腰直角三角形時,∠FOC= ;
②求證:OE=OF;
(2)如圖②,若AO:AC=1:4時,OE和OF有怎樣的數量關系?證明你發現的結論.

查看答案和解析>>
科目:初中數學 來源: 題型:
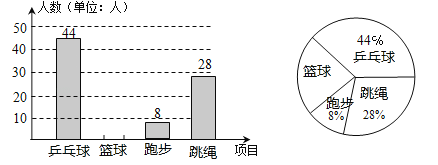
【題目】某校開展“陽光體育”活動,決定開設乒乓球、籃球、跑步、跳繩這四種運動項目,學生只能選擇其中一種,為了解學生喜歡哪一種項目,隨機抽取了部分學生進行調查,并將調查結果繪制成兩張不完整的統計圖,請你結合圖中的信息解答下列問題:
(1)樣本中喜歡籃球項目的人數百分比是 ;其所在扇形統計圖中的圓心角的度數是 ;
(2)把條形統計圖補畫完整并注明人數;
(3)已知該校有1000名學生,根據樣本估計全校喜歡乒乓球的人數是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,平行四邊形ABCD中,∠B=60°,AB=8cm,AD=10cm,點P在邊BC上從B向C運動,點Q在邊DA上從D向A運動,如果P,Q運動的速度都為每秒1cm,那么當運動時間t=_____秒時,四邊形ABPQ是直角梯形.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,點E、F分別在邊AB、BC上,且AE=![]() AB=2,將矩形沿直線EF折疊,點B恰好落在AD邊上的點P處,連接BP交EF于點Q,下列結論:①EF=2BE;②△APE≌△QEB;③FQ=3EQ;④SBFPE=8
AB=2,將矩形沿直線EF折疊,點B恰好落在AD邊上的點P處,連接BP交EF于點Q,下列結論:①EF=2BE;②△APE≌△QEB;③FQ=3EQ;④SBFPE=8![]() ,其中正確的結論是______(只填序號).
,其中正確的結論是______(只填序號).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在梯形ABCD中,AD∥BC,AB=CD,BC=10,對角線AC、BD相交于點O,且AC⊥BD,設AD=x,△AOB的面積為y.
(1)求∠DBC的度數;
(2)求y關于x的函數解析式,并寫出自變量x的取值范圍;
(3)如圖1,設點P、Q分別是邊BC、AB的中點,分別聯結OP,OQ,PQ.如果△OPQ是等腰三角形,求AD的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了慶祝新中國成立70周年,某校組織八年級全體學生參加“恰同學少年,憶崢嶸歲月”新中國成立70周年知識競賽活動.將隨機抽取的部分學生成績進行整理后分成5組,50~60分(![]() )的小組稱為“學童”組,60~70分(
)的小組稱為“學童”組,60~70分(![]() )的小組稱為“秀才”組,70~80分(
)的小組稱為“秀才”組,70~80分(![]() )的小組稱為“舉人”組,80~90分(
)的小組稱為“舉人”組,80~90分(![]() )的小組稱為“進士”組,90~100分(
)的小組稱為“進士”組,90~100分(![]() )的小組稱為“翰林”組,并繪制了不完整的頻數分布直方圖如下,請結合提供的信息解答下列問題:
)的小組稱為“翰林”組,并繪制了不完整的頻數分布直方圖如下,請結合提供的信息解答下列問題:
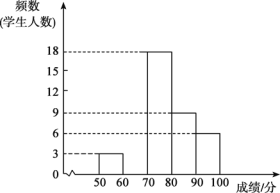
(1)若“翰林”組成績的頻率是12.5%,請補全頻數分布直方圖;
(2)在此次比賽中,抽取學生的成績的中位數在 組;
(3)學校決定對成績在70~100分(![]() )的學生進行獎勵,若八年級共有336名學生,請通過計算說明,大約有多少名學生獲獎?
)的學生進行獎勵,若八年級共有336名學生,請通過計算說明,大約有多少名學生獲獎?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com