
教材中第25章銳角的三角比,在這章的小結中有如下一段話:銳角三角比定量地描述了在直角三角形中邊角之間的聯系.在直角三角形中,一個銳角的大小與兩條邊長的比值相互唯一確定,因此邊長與角的大小之間可以相互轉化.
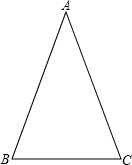
類似的,可以在等腰三角形中建立邊角之間的聯系,我們定義:等腰三角形中底邊與腰的比叫做頂角的正對(sad).如圖,在△ABC中,AB=AC,頂角A的正對記作sadA,這時
sad A= .容易知道一個角的大小與這個角的正對值也是相互唯一確定的.
.容易知道一個角的大小與這個角的正對值也是相互唯一確定的.
根據上述對角的正對定義,解下列問題:

(1)sad  的值為( ▼ )
的值為( ▼ )
A.  B.
1 C.
B.
1 C.  D.
2
D.
2
(2)對于 ,∠A的正對值sad A的取值范圍是 ▼ .
,∠A的正對值sad A的取值范圍是 ▼ .
(3)已知 ,其中
,其中 為銳角,試求sad
為銳角,試求sad 的值.
的值.
(1)B
(2)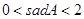
(3)sad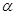
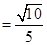
【解析】解:(1)B;----------------------------------------------(4分)
(2)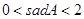 ;------------------------------------(4分)
;------------------------------------(4分)
(3) 如圖,在△ABC中,∠ACB=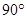 ,sin∠A
,sin∠A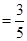 .
.
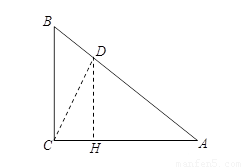
在AB上取點D,使AD=AC,
作DH⊥AC,H為垂足,令BC =3k,AB =5k,
則AD= AC=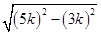 =4k,-------(1分)
=4k,-------(1分)
又在△ADH中,∠AHD=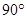 ,sin∠A
,sin∠A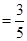 .
.
∴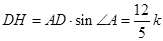 ,
,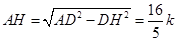 .
.
則在△CDH中,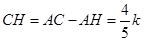 ,
,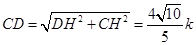 .---(2分)
.---(2分)
于是在△ACD中,AD= AC=4k,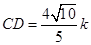 .
.
由正對定義可得:sadA=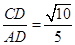 ,即sad
,即sad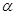
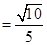 .------(1分)
.------(1分)


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
| 底邊 |
| 腰 |
| BC |
| AB |
 互唯一確定的.
互唯一確定的.| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 5 |
查看答案和解析>>
科目:初中數學 來源: 題型:
教材中第25章銳角的三角比,在這章的小結中有如下一段話:銳角三角比定量地描述了在直角三角形中邊角之間的聯系.在直角三角形中,一個銳角的大小與兩條邊長的比值相互唯一確定,因此邊長與角的大小之間可以相互轉化.
類似的,可以在等腰三角形中建立邊角之間的聯系,我們定義:等腰三角形中底邊與腰的比叫做頂角的正對(sad).如圖,在△ABC中,AB=AC,頂角A的正對記作sadA,這時
sad A=.容易知道一個角的大小與這個角的正對值也是相互唯一確定的.
根據上述對角的正對定義,解下列問題:

(1)sad 的值為( ▼ )
A. B.1 C.
D.2
(2)對于,∠A的正對值sad A的取值范圍是 ▼ .
(3)已知,其中
為銳角,試求sad
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
 .容易知道一個角的大小與這個角的正對值也是相互唯一確定的.
.容易知道一個角的大小與這個角的正對值也是相互唯一確定的.
 的值為( ▼ )
的值為( ▼ )A. | B.1 | C. | D.2 |
 ,∠A的正對值sad A的取值范圍是 ▼ .
,∠A的正對值sad A的取值范圍是 ▼ . ,其中
,其中 為銳角,試求sad
為銳角,試求sad 的值.
的值.查看答案和解析>>
科目:初中數學 來源:2011屆北京市昌平區初三上學期期末考試數學卷 題型:解答題
教材中第25章銳角的三角比,在這章的小結中有如下一段話:銳角三角比定量地描述了在直角三角形中邊角之間的聯系.在直角三角形中,一個銳角的大小與兩條邊長的比值相互唯一確定,因此邊長與角的大小之間可以相互轉化.
類似的,可以在等腰三角形中建立邊角之間的聯系,我們定義:等腰三角形中底邊與腰的比叫做頂角的正對(sad).如圖,在△ABC中,AB=AC,頂角A的正對記作sadA,這時
sad A= .容易知道一個角的大小與這個角的正對值也是相互唯一確定的.
.容易知道一個角的大小與這個角的正對值也是相互唯一確定的.
根據上述對角的正對定義,解下列問題:
(1)sad  的值為( ▼ )
的值為( ▼ )
A. | B.1 | C. | D.2 |
 ,∠A的正對值sad A的取值范圍是 ▼ .
,∠A的正對值sad A的取值范圍是 ▼ . ,其中
,其中 為銳角,試求sad
為銳角,試求sad 的值.
的值.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com