
【題目】觀察如圖圖形,把一個三角形分別連接其三邊中點,構成4個小三角形,挖去中間的一個小三角形(如圖1),對剩下的三個小三角形再分別重復以上做法,……,據此解答下面的問題
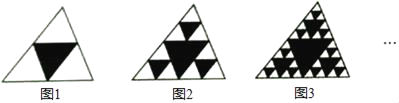
(1)填寫下表:
圖形 | 挖去三角形的個數 |
圖形1 | 1 |
圖形2 | 1+3 |
圖形3 | 1+3+9 |
圖形4 |
|
(2)根據這個規律,求圖n中挖去三角形的個數wn;(用含n的代數式表示)
(3)若圖n+1中挖去三角形的個數為wn+1,求wn+1﹣Wn
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
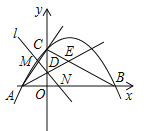
【題目】(2017南寧,第26題,10分)如圖,已知拋物線![]() 與坐標軸交于A,B,C三點,其中C(0,3),∠BAC的平分線AE交y軸于點D,交BC于點E,過點D的直線l與射線AC,AB分別交于點M,N.
與坐標軸交于A,B,C三點,其中C(0,3),∠BAC的平分線AE交y軸于點D,交BC于點E,過點D的直線l與射線AC,AB分別交于點M,N.
(1)直接寫出a的值、點A的坐標及拋物線的對稱軸;
(2)點P為拋物線的對稱軸上一動點,若△PAD為等腰三角形,求出點P的坐標;
(3)證明:當直線l繞點D旋轉時,![]() 均為定值,并求出該定值.
均為定值,并求出該定值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀理解
在△ABC中,AB、BC、AC三邊的長分別為![]() 、
、![]() 、2,求這個三角形的面積.
、2,求這個三角形的面積.
解法一:如圖1,因為△ABC是等腰三角形,并且底AC=2,根據勾股定理可以求得底邊的高AF為1,所以S△ABC=![]() ×2×1=1.
×2×1=1.
解法二:建立邊長為1的正方形網格,在網格中畫出△ABC,使△ABC三個頂點都在小正方形的頂點處,如圖2所示,借用網格面積可得S△ABC=S矩形ADEC﹣S△ABD﹣S△EBC=1.
方法遷移:請解答下面的問題:
在△ABC中,AB、AC、BC三邊的長分別為![]() 、
、![]() 、
、![]() ,求這個三角形的面積.
,求這個三角形的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,C是AB的中點,D是BE的中點,

(1)AB=4cm,BE=3cm,則CD=____________cm;
(2)AB=4cm,DE=2cm,則AE=____________cm;
(3)AB=4cm,BE=2cm,則AD=____________cm;
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,一次函數y1=x+2與反比例函數y2=![]() (x>0)的圖象交于點A(a,5)
(x>0)的圖象交于點A(a,5)
(1)確定反比例函數的表達式;
(2)結合圖象,直接寫出x為何值時,y1<y2
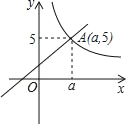
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】綠水青山就是金山銀山,國家倡導全民植樹。在今年3月12日植樹節當天,某校七年級一班48名學生全部參加了植樹活動,男生每人栽種4株,女生每人栽種3株,全班共栽種170株。
(1)該班男、女生各為多少人?
(2)學校選擇購買甲、乙兩種樹苗,甲樹苗![]() ,乙樹苗
,乙樹苗![]() .如果要使購買樹苗的錢不超過1200元,那么最多可以購買甲樹苗多少株?
.如果要使購買樹苗的錢不超過1200元,那么最多可以購買甲樹苗多少株?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠C=90°,AD平分∠CAB,交CB于點D,過點D作DE⊥AB,于點E
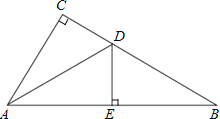
(1)求證:△ACD≌△AED;
(2)若∠B=30°,CD=1,求BD的長。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知如圖,點 C 在以 AB 為直徑的⊙O 上,點 D 在 AB 的延長線上,∠BCD =∠A.
(1)求證:CD 為⊙O 的切線;
(2)過點 C 作 CE⊥AB 于點 E.若 CE = 2,cos D =![]() ,求 AD 的長.
,求 AD 的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】恩施州綠色、富硒產品和特色農產品在國際市場上頗具競爭力,其中香菇遠銷日本和韓國等地.上市時,外商李經理按市場價格10元/千克在我州收購了2000千克香菇存放入冷庫中.據預測,香菇的市場價格每天每千克將上漲0.5元,但冷庫存放這批香菇時每天需要支出各種費用合計340元,而且香菇在冷庫中最多保存110天,同時,平均每天有6千克的香菇損壞不能出售.
(1)若存放x天后,將這批香菇一次性出售,設這批香菇的銷售總金額為y元,試寫出y與x之間的函數關系式.
(2)李經理想獲得利潤22500元,需將這批香菇存放多少天后出售?(利潤=銷售總金額﹣收購成本﹣各種費用)
(3)李經理將這批香菇存放多少天后出售可獲得最大利潤?最大利潤是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com