
【題目】閱讀下面材料并解決有關問題:
我們知道:|x|=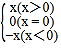 .現在我們可以用這一結論來化簡含有絕對值的代數式,現在我們可以用這一結論來化簡含有絕對值的代數式,如化簡代數式|x+1|+|x﹣2|時,可令x+1=0和x﹣2=0,分別求得x=﹣1,x=2(稱﹣1,2分別為|x+1|與|x﹣2|的零點值).在實數范圍內,零點值x=﹣1和,x=2可將全體實數分成不重復且不遺漏的如下3種情況:
.現在我們可以用這一結論來化簡含有絕對值的代數式,現在我們可以用這一結論來化簡含有絕對值的代數式,如化簡代數式|x+1|+|x﹣2|時,可令x+1=0和x﹣2=0,分別求得x=﹣1,x=2(稱﹣1,2分別為|x+1|與|x﹣2|的零點值).在實數范圍內,零點值x=﹣1和,x=2可將全體實數分成不重復且不遺漏的如下3種情況:
①x<﹣1;②﹣1≤x<2;③x≥2.
從而化簡代數式|x+1|+|x﹣2|可分以下3種情況:
①當x<﹣1時,原式=﹣(x+1)﹣(x﹣2)=﹣2x+1;
②當﹣1≤x<2時,原式=x+1﹣(x﹣2)=3;
③當x≥2時,原式=x+1+x﹣2=2x﹣1.綜上討論,原式=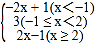 .
.
通過以上閱讀,請你解決以下問題:
(1)化簡代數式|x+2|+|x﹣4|.
(2)求|x﹣1|﹣4|x+1|的最大值.
【答案】(1)原式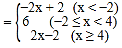 ;(2)
;(2)![]() 的最大值為2.
的最大值為2.
【解析】
(1)分為x<﹣2、﹣2≤x<4、x≥4三種情況化簡即可;
(2)分x<﹣1、﹣1≤x≤1、x>1分別化簡,結合x的取值范圍確定代數式值的范圍,從而求出代數式的最大值.
(1)令![]() 和
和![]() ,分別求得
,分別求得![]() ,x=4,(稱-2,4分別為
,x=4,(稱-2,4分別為![]() 和
和![]() 的零點值).
的零點值).
在實數范圍內,零點值![]() 和
和![]() ,可將全體實數分成不重復且不遺漏的如下3種情況:
,可將全體實數分成不重復且不遺漏的如下3種情況:
(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
從而化簡代數式![]() 可分以下3種情況:
可分以下3種情況:
(1)當![]() 時,原式
時,原式![]() ;
;
(2)當![]() 時,原式
時,原式![]() ;
;
(3)當![]() 時,原式
時,原式![]() .
.
綜上所述:原式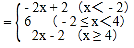 .
.
(2)令x-1=0和x+1=0,分別求得x=1,x=-1.
在實數范圍內,零點值x=-1和x=1,可將全體實數分成不重復且不遺漏的如下3種情況:
(1)x<-1;(2)![]() ;(3)
;(3)![]() .
.
從而化簡代數式![]() 可分以下3種情況:
可分以下3種情況:
(1)當![]() 時,原式
時,原式![]() ;
;
(2)當![]() 時,原式
時,原式![]() ;
;
(3)當x>1時,原式![]() .
.
綜上所述:![]() 的最大值為2.
的最大值為2.


科目:初中數學 來源: 題型:
【題目】某實驗學校為開展研究性學習,準備購買一定數量的兩人學習桌和三人學習桌,如果購買3張兩人學習桌,1張三人學習桌需220元;如果購買2張兩人學習桌,3張三人學習桌需310元.
(1)求兩人學習桌和三人學習桌的單價;
(2)學校欲投入資金不超過6000元,購買兩種學習桌共98張,以至少滿足248名學生的需求,設購買兩人學習桌x張,購買兩人學習桌和三人學習桌的總費用為W 元,求出W與x的函數關系式;求出所有的購買方案.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,D、E、F分別是△ABC的邊AB、BC、AC的中點.若四邊形ADEF是菱形,則△ABC必須滿足的條件是( ) 
A.AB⊥AC
B.AB=AC
C.AB=BC
D.AC=BC
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為方便市民出行,減輕城市中心交通壓力,長沙市正在修建貫穿星城南北、東西的地鐵1、2號線.已知修建地鐵1號線24千米和2號線22千米共需投資265億元;若1號線每千米的平均造價比2號線每千米的平均造價多0.5億元.
(1)求1號線,2號線每千米的平均造價分別是多少億元?
(2)除1、2號線外,長沙市政府規劃到2018年還要再建91.8千米的地鐵線網.據預算,這91.8千米地鐵線網每千米的平均造價是1號線每千米的平均造價的1.2倍,則還需投資多少億元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】目前,步行已成為人們最喜愛的健身方法之一,通過手機可以計算行走的步數與相應的能量消耗.對比手機數據發現小明步行12 000步與小紅步行9 000步消耗的能量相同.若每消耗1千卡能量小明行走的步數比小紅多10步,求小紅每消耗1千卡能量需要行走多少步?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】請從以下兩個小題中任選一個作答,若多選,則按所選的第一小題計分.
①若單項式﹣xmyn+4 與 5x2y 是同類項,則 nm 的值為____.
②實施西部大開發戰略是黨中央的重大決策,我國國土面積約為960 萬平方千米,而我國西部地區的面積占我國國土面積的 ![]() ,用科學記數法表示我國西部地區的面積約為_____平方千米.
,用科學記數法表示我國西部地區的面積約為_____平方千米.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明計劃三天看完一本書,預計第一天看 x 頁,第二天看的頁數比第一天看的頁數多50 頁,第三天看的頁數比第二天看的頁數的一半還少5頁.
(1)用含x的式子表示這本書的頁數;
(2)若 x=100,則這本書共有多少頁?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,CB=CA,∠ACB=90°,點D在邊BC上(與B,C不重合),四邊形ADEF為正方形,過點F作FG⊥CA,交CA的延長線于點G,連接FB,交DE于點Q,給出以下結論:①AC=FG;②S△FAB∶S四邊形CBFG=1∶2;③∠ABC=∠ABF;④AD2=FQ·AC,其中正確結論的個數是( )

A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,AB=CD,BF=DE,AE⊥BD,CF⊥BD,垂足分別為E,F.

(1)求證:△ABE≌△CDF;
(2)若AC與BD交于點O,求證:AO=CO.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com