
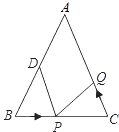
【題目】如圖,已知△ABC中,∠B=∠C,AB=AC=10cm,BC=8cm,點D為AB的中點.
(1)如果點P在線段BC上以3cm/s的速度由B點向C點運動,同時,點Q在線段CA上由C點向A點運動.
①若點Q的運動速度與點P的運動速度相等,經過1s后,△BPD與△CQP是否全等,請說明理由;
②若點Q的運動速度與點P的運動速度不相等,當點Q的運動速度為多少時,能夠使△BPD與△CQP全等?
(2)若點Q以②中的運動速度從點C出發,點P以原來的運動速度從點B同時出發,都逆時針沿△ABC三邊運動,求經過多長時間點P與點Q第一次在△ABC邊上相遇?
【答案】(1)全等,理由見解析;(2)![]() ,(3)
,(3)![]() .
.
【解析】試題分析:(1)①根據時間和速度分別求得兩個三角形中的邊的長,根據SAS判定兩個三角形全等.
②根據全等三角形應滿足的條件探求邊之間的關系,再根據路程=速度×時間公式,先求得點P運動的時間,再求得點Q的運動速度;
(2)根據題意結合圖形分析發現:由于點Q的速度快,且在點P的前邊,所以要想第一次相遇,則應該比點P多走等腰三角形的兩個腰長.
試題解析:(1)①∵t=1s,
∴BP=CQ=3×1=3cm,
∵AB=10cm,點D為AB的中點,
∴BD=5cm.
又∵PC=BC﹣BP,BC=8cm,
∴PC=8﹣3=5cm,
∴PC=BD.
又∵AB=AC,
∴∠B=∠C,
在△BPD和△CQP中,  ,
,
∴△BPD≌△CQP(SAS).
②∵vP≠vQ,
∴BP≠CQ,
若△BPD≌△CPQ,∠B=∠C,
則BP=PC=4cm,CQ=BD=5cm,
∴點P,點Q運動的時間![]() ,
,
∴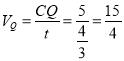 cm/s;
cm/s;
(2)設經過x秒后點P與點Q第一次相遇,
由題意,得![]() x=3x+2×10,
x=3x+2×10,
解得![]() .
.
∴點P共運動了![]() ×3=80cm.
×3=80cm.
△ABC周長為:10+10+8=28cm,
若是運動了三圈即為:28×3=84cm,
∵84﹣80=4cm<AB的長度,
∴點P、點Q在AB邊上相遇,
∴經過![]() s點P與點Q第一次在邊AB上相遇.
s點P與點Q第一次在邊AB上相遇.


 考前必練系列答案
考前必練系列答案科目:初中數學 來源: 題型:
【題目】過度包裝既浪費資源又污染環境.據測算,如果全國每年減少10%的過度包裝紙用量,那么可減排二氧化碳3120000噸,把數3120000用科學記數法表示為( )
A. 3.12×105 B. 3.12×106 C. 31.2×105 D. 0.312×107
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】幼兒園的小朋友打算選擇一種形狀、大小都相同的多邊形塑料膠板鋪地面.為了保證鋪地時既無縫隙,又不重疊,請你告訴他們可以選擇哪些形狀的塑料膠板(填三種) .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABD和△ACE中,有下列四個等式:①AB=AC;②AD=AE;③∠1=∠2;④BD=CE.以其中三個條件為題設,填入已知欄中,一個論斷為結論,填入下面求證欄中,使之組成一個真命題,并寫出證明過程.
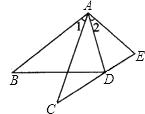
已知: .
求證: .
證明:
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com