
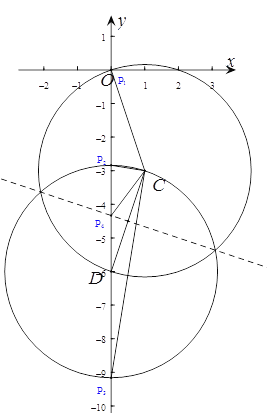
【題目】已知直線y=2x-5與x軸和y軸分別交于點A和點B,點C(1,n)在直線AB上,點D在y軸的負半軸上,且CD=![]() .
.
(1)求點C、點D的坐標.
(2)若P為y軸上的點,當△PCD為等腰三角形時,求點P的坐標.
(3)若點M為x軸上一動點(點M不與點O重合),N為直線y=2x-5上一動點,是否存在點M、N,使得△AMN與△AOB全等?若存在,求出點N的坐標;若不存在,請說明理由.


圖1 圖2
【答案】(1)C(1,-3),D(0,-6);(2)P(0, ![]() ) 、P(0,
) 、P(0, ![]() ) 、P(0,0)、P(0,
) 、P(0,0)、P(0, ![]() );(3)N(5,5)或N(
);(3)N(5,5)或N(![]() )或N(
)或N(![]() ).
).
【解析】試題分析:(1)先確定點C的坐標,設點D坐標為(0,d)(d<0),則有CD2=(1-0)2+(-3-d)2=![]() ,解之即可得;
,解之即可得;
(2)分別以點C、點D為圓心,CD為半徑畫圓,圓與y軸即為滿足條件的點,作CD的中垂線與y軸的交點也滿足條件,然后根據CD的長以及等腰三角形的性質即可得;
(3)分△AM1N1≌△AOB與△AM1N1≌△ABO兩種情況,畫出相應的圖形進行求解即可得.
試題解析:(1)當x=1時,y=2x-5=-3,所以C(1,-3),
設點D坐標為(0,d)(d<0),則有CD2=(1-0)2+(-3-d)2=![]() ,解得:d=0(舍去)或d=-6,所以D(0,-6);
,解得:d=0(舍去)或d=-6,所以D(0,-6);
(2)當P1C=CD時,由(1)計算可知此時P1與原點O重合,所以P1(0,0),
當PC為底時,如圖,此時PD=CD=![]() ,所以P2(0,-6-
,所以P2(0,-6-![]() )、P3(0,-6+
)、P3(0,-6+![]() ),
),
當CD為底邊時,設P點坐標為(0,p),由題意則有(-3-p)2+12=(-6-p)2,解得:p=![]() ,所以P4(0,
,所以P4(0, ![]() ),
),
綜上,點P坐標為: P1(0,0)、P2(0, ![]() ) 、P3(0,
) 、P3(0, ![]() )、P4(0,
)、P4(0, ![]() );
);
(3)由y=2x-5與x軸和y軸分別交于點A和點B可知OA=2.5,OB=5,AB=![]() ,
,
如圖所示,當△AM1N1≌△AOB時,AM=AO,M1N1=OB,所以N1(5,5),
當△AM1N1≌△ABO時,AN3=AO=2.5,過點N3作N3E2⊥OA,
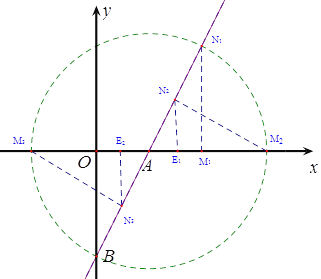
則有△AE2N3∽△AOB,∴![]() ,
,
即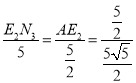 ,∴E2N3=
,∴E2N3=![]() ,AE2=
,AE2=![]() ,
,
同理E1N2=![]() ,AE1=
,AE1=![]() ,
,
∴N3(![]() ),N2(
),N2(![]() ),
),
綜上,點N的坐標為:N1(5,5),N2(![]() ),N3(
),N3(![]() ).
).


科目:初中數學 來源: 題型:
【題目】如圖,圓桌正上方的燈泡(看作一個點)發出的光線照射桌面后,在地面上形成陰影.已知桌面的直徑為1.2 m,桌面距離地面1 m.若燈泡距離地面3 m,則地面上陰影部分的面積為 ( )

A. 0.36πm2 B. 0.81πm2 C. 2πm2 D. 3.24πm2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】八(1)班同學為了解2015年某小區家庭月均用水情況,隨機調查了該小區部分家庭,并將調查數據進行如下整理,
月均用水量 | 頻數(戶) | 頻率 |
| 6 | 0.12 |
| m | 0.24 |
| 16 | 0.32 |
| 10 | 0.20 |
| 4 | n |
| 2 | 0.04 |
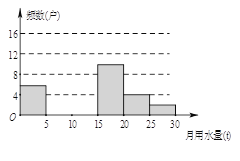
請解答以下問題:
(1)這里采用的調查方式是 (填“普查”或“抽樣調查”),樣本容量是 ;
(2)填空: ![]() ,
, ![]() ,并把頻數分布直方圖補充完整;
,并把頻數分布直方圖補充完整;
(3)若將月均用水量的頻數繪成扇形統計圖,則月均用水量“
(4)若該小區有1000戶家庭,求該小區月均用水量超過10t的家庭大約有多少戶?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲,乙兩人同時各接受了600個零件的加工任務,甲比乙每分鐘加工的數量多,兩人同時開始加工,加工過程中其中一人因故障停止加工幾分鐘后又繼續按原速加工,直到他們完成任務,如圖表示甲比乙多加工的零件數量![]() (個)與加工時間
(個)與加工時間![]() (分)之間的函數關系,觀察圖象解決下列問題:
(分)之間的函數關系,觀察圖象解決下列問題:
(1)點B的坐標是________,B點表示的實際意義是___________ _____;
(2)求線段BC對應的函數關系式和D點坐標;
(3)乙在加工的過程中,多少分鐘時比甲少加工100個零件?
(4)為了使乙能與甲同時完成任務,現讓丙幫乙加工,直到完成.丙每分鐘能加工3個零件,并把丙加工的零件數記在乙的名下,問丙應在第多少分鐘時開始幫助乙?并在圖中用虛線畫出丙幫助后y與x之間的函數關系的圖象.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點C是線段AB上一點,△ACD和△BCE都是等邊三角形,連結AE,BD,設AE交CD于點F.
(1)求證:△ACE≌△DCB;
(2)求證:△ADF∽△BAD.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某一工程,在工程招標時,接到甲、乙兩個工程隊的投標書.施工一天,需付甲工程隊工程款1.2萬元,乙工程隊工程款0.5萬元.工程領導小組根據甲、乙兩隊的投標書測算,有如下方案:①甲隊單獨完成這項工程剛好如期完成;②乙隊單獨完成這項工程要比規定日期多用6天;③若甲、乙兩隊合做3天,余下的工程由乙隊單獨做也正好如期完成.試問:
(1)兩隊單獨做各要幾天完成?
(2)在不耽誤工期的前提下,你覺得哪一種施工方案最節省工程款?請說明理.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】補全下列各題解題過程.
如圖,EF∥AD,∠1 = ∠2,∠BAC = 70°,求 ∠AGD 的度數.

解:∵EF∥AD ( 已知 )
∴∠2 = ( )
又∵∠1=∠2 ( )
∴∠1=∠3 ( )
∴AB∥ ( )
∴∠BAC + = 180°( )
∵∠BAC = 70°(已知 )
∴∠AGD = _ .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,Rt△OAB如圖所示放置在平面直角坐標系中,直角邊OA與x軸重合,∠OAB=90°,OA=4,AB=2,把Rt△OAB繞點O逆時針旋轉90°,點B旋轉到點C的位置,一條拋物線正好經過點O,C,A三點.
(1)求該拋物線的解析式;
(2)在x軸上方的拋物線上有一動點P,過點P作x軸的平行線交拋物線于點M,分別過點P,點M作x軸的垂線,交x軸于E,F兩點,問:四邊形PEFM的周長是否有最大值?如果有,請求出最值,并寫出解答過程;如果沒有,請說明理由.
(3)如果x軸上有一動點H,在拋物線上是否存在點N,使O(原點)、C、H、N四點構成以OC為一邊的平行四邊形?若存在,求出N點的坐標;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com