
【題目】如圖,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分線.以O為圓心,OC為半徑作⊙O.
(1)求證:AB是⊙O的切線.
(2)已知AO交⊙O于點E,延長AO交⊙O于點D,tanD=![]() ,求
,求![]() 的值.
的值.
(3)(3分)在(2)的條件下,設⊙O的半徑為3,求AB的長.

【答案】(1)證明見解析;(2)![]() ;(3)
;(3)![]()
【解析】試題分析:(1)過O作OF⊥AB于F,由角平分線上的點到角兩邊的距離相等即可得證;(2)連接CE,證明△ACE∽△ADC可得![]() = tanD=
= tanD=![]() ;(3)先由勾股定理求得AE的長,再證明△B0F∽△BAC,得
;(3)先由勾股定理求得AE的長,再證明△B0F∽△BAC,得![]() ,設BO="y" ,BF=z,列二元一次方程組即可解決問題.
,設BO="y" ,BF=z,列二元一次方程組即可解決問題.
試題解析:(1)證明:作OF⊥AB于F
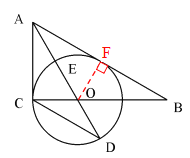
∵AO是∠BAC的角平分線,∠ACB=90
∴OC=OF
∴AB是⊙O的切線
(2)連接CE
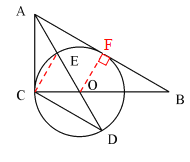
∵AO是∠BAC的角平分線,
∴∠CAE=∠CAD
∵∠ACE所對的弧與∠CDE所對的弧是同弧
∴∠ACE=∠CDE
∴△ACE∽△ADC
∴![]() = tanD=
= tanD=![]()
(3)先在△ACO中,設AE=x,
由勾股定理得
(x+3)="(2x)" +3 ,解得x="2,"
∵∠BFO=90°=∠ACO
易證Rt△B0F∽Rt△BAC
得![]() ,
,
設BO=y BF=z
![]()
即4z=9+3y,4y=12+3z
解得z=![]() y=
y=![]()
∴AB=![]() +4=
+4=![]()


科目:初中數學 來源: 題型:
【題目】在平面直角坐標系XOY中,有A(3 , 2) ,B (-1 ,-4 ),P是X軸上的一點,Q是Y軸上的一點,若以點A,B,P,Q四個點為頂點的四邊形是平行四邊形,則Q點的坐標是______.
查看答案和解析>>
科目:初中數學 來源: 題型:
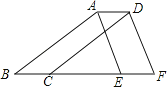
【題目】如圖將△ABE向右平移3 cm得到△DCF,已知△ABE的周長是16 cm.
(1)試判斷AD與EF的關系,并證明.
(2)求四邊形ABFD的周長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列計算中,正確的是( )
A. (-2)-(-5)=-7 B. (-2)+(-3)=-1
C. (-2)×(-3)=6 D. (-12)÷(-2)=-6
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知二次函數y=ax2+bx+c(a≠0)的圖象與x軸交于點A(﹣1,0),與y軸的交點B在(0,﹣2)和(0,﹣1)之間(不包括這兩點),對稱軸為直線x=1.下列結論:①abc>0 ②4a+2b+c>0 ③4ac﹣b2<8a ④![]() <a<
<a<![]() ⑤b>c.其中含所有正確結論的選項是( )
⑤b>c.其中含所有正確結論的選項是( )
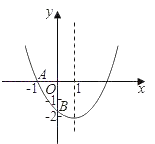
A. ①③ B. ①③④ C. ②④⑤ D. ①③④⑤
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法:①數軸上的點對應的數,如果不是有理數,那么一定是無理數;②介于4與5之間的無理數有無數個; ③數軸上的任意一點表示的數都是有理數;④任意一個有理數都可以用數軸上的點表示.其中正確的有( )
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com