
【題目】(1)問(wèn)題探究:如圖①,在四邊形ABCD中,AB∥CD,E是BC的中點(diǎn),AE是∠BAD的平分線(xiàn),則線(xiàn)段AB,AD,DC之間的等量關(guān)系為 ;
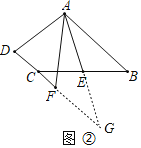
(2)方法遷移:如圖②,在四邊形ABCD中,AB∥CD,AF與DC的延長(zhǎng)線(xiàn)交于點(diǎn)F,E是BC的中點(diǎn),AE是∠BAF的平分線(xiàn),試探究線(xiàn)段AB,AF,CF之間的等量關(guān)系,并證明你的結(jié)論;
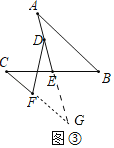
(3)聯(lián)想拓展:如圖③,AB∥CF,E是BC的中點(diǎn),點(diǎn)D在線(xiàn)段AE上,∠EDF=∠BAE,試探究線(xiàn)段AB,DF,CF之間的數(shù)量關(guān)系,并證明你的結(jié)論.

【答案】(1)AD=AB+DC;(2)AB=AF+CF,證明詳見(jiàn)解析;(3)AB=DF+CF,證明詳見(jiàn)解析.
【解析】
(1)結(jié)論:AD=AB+DC.延長(zhǎng)AE,DC交于點(diǎn)F,證明△ABE≌△FEC(AAS),即可推出AB=CF,再證明DA=DF,即可解決問(wèn)題.
(2)結(jié)論:AB=AF+CF,如圖②,延長(zhǎng)AE交DF的延長(zhǎng)線(xiàn)于點(diǎn)G,證明方法類(lèi)似(1).
(3)結(jié)論;AB=DF+CF.如圖③,延長(zhǎng)AE交CF的延長(zhǎng)線(xiàn)于點(diǎn)G,證明方法類(lèi)似(1).
解:(1)探究問(wèn)題:結(jié)論:AD=AB+DC.
理由:如圖①中,延長(zhǎng)AE,DC交于點(diǎn)F,

∵AB∥CD,
∴∠BAF=∠F,
在△ABE和△FCE中,
CE=BE,∠BAF=∠F,∠AEB=∠FEC,
∴△ABE≌△FEC(AAS),
∴CF=AB,
∵AE是∠BAD的平分線(xiàn),
∴∠BAF=∠FAD,
∴∠FAD=∠F,
∴AD=DF,
∵DC+CF=DF,
∴DC+AB=AD.
故答案為AD=AB+DC.
(2)方法遷移:結(jié)論:AB=AF+CF.
證明:如圖②,延長(zhǎng)AE交DF的延長(zhǎng)線(xiàn)于點(diǎn)G,
∵E是BC的中點(diǎn),
∴CE=BE,
∵AB∥DC,
∴∠BAE=∠G.且BE=CE,∠AEB=∠GEC
∴△AEB≌△GEC(AAS)
∴AB=GC
∵AE是∠BAF的平分線(xiàn)
∴∠BAG=∠FAG,
∵∠BAG∠G,
∴∠FAG=∠G,
∴FA=FG,
∵CG=CF+FG,
∴AB=AF+CF.
(3)聯(lián)想拓展:結(jié)論;AB=DF+CF.
證明:如圖③,延長(zhǎng)AE交CF的延長(zhǎng)線(xiàn)于點(diǎn)G,
∵E是BC的中點(diǎn),
∴CE=BE,
∵AB∥CF,
∴∠BAE=∠G,
在△AEB和△GEC中,
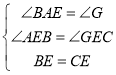 ,
,
∴△AEB≌△GEC,
∴AB=GC,
∵∠EDF=∠BAE,
∴∠FDG=∠G,
∴FD=FG,
∴AB=DF+CF.


 閱讀快車(chē)系列答案
閱讀快車(chē)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,△ABC是⊙O的內(nèi)接三角形,AB=AC,∠BCA=65°,作CD∥AB,并與○O相交于點(diǎn)D,連接BD,則∠DBC的大小為

A. 15° B. 35° C. 25° D. 45°
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,∠ABC=∠ADC=90°,∠BAD=45°,E、F分別是AC、BD的中點(diǎn).若AC=2,求EF的長(zhǎng).

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,
,![]() 平分
平分![]() 交
交![]() 于
于![]() 點(diǎn).
點(diǎn).

(1)如圖①,若![]() 于
于![]() 點(diǎn),
點(diǎn),![]() ,求
,求![]() 的度數(shù);
的度數(shù);
(2)如圖②,若![]() 交
交![]() 于
于![]() 點(diǎn),求證:
點(diǎn),求證:![]() .
.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖![]() ,二次函數(shù)
,二次函數(shù)![]() 的圖象與
的圖象與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,與
,與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,過(guò)點(diǎn)
,過(guò)點(diǎn)![]() 作
作![]() 軸,交拋物線(xiàn)于點(diǎn)
軸,交拋物線(xiàn)于點(diǎn)![]() ,并過(guò)點(diǎn)
,并過(guò)點(diǎn)![]() 作
作![]() 軸,垂足為
軸,垂足為![]() .拋物線(xiàn)
.拋物線(xiàn)![]() 和反比例函數(shù)
和反比例函數(shù)![]() 的圖象都經(jīng)過(guò)點(diǎn)
的圖象都經(jīng)過(guò)點(diǎn)![]() ,四邊形
,四邊形![]() 的面積是
的面積是![]() .
.
![]() 求反比例函數(shù)、二次函數(shù)的解析式及拋物線(xiàn)的對(duì)稱(chēng)軸;
求反比例函數(shù)、二次函數(shù)的解析式及拋物線(xiàn)的對(duì)稱(chēng)軸;
![]() 如圖
如圖![]() ,點(diǎn)
,點(diǎn)![]() 從
從![]() 點(diǎn)出發(fā)以每秒
點(diǎn)出發(fā)以每秒![]() 個(gè)單位的速度沿線(xiàn)段
個(gè)單位的速度沿線(xiàn)段![]() 向
向![]() 點(diǎn)運(yùn)動(dòng),點(diǎn)
點(diǎn)運(yùn)動(dòng),點(diǎn)![]() 從
從![]() 點(diǎn)出發(fā)以相同的速度沿線(xiàn)段img src="http://thumb.zyjl.cn/questionBank/Upload/2019/05/12/08/1a8f9afd/SYS201905120854095644903087_ST/SYS201905120854095644903087_ST.023.png" width="24" height="19" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />向
點(diǎn)出發(fā)以相同的速度沿線(xiàn)段img src="http://thumb.zyjl.cn/questionBank/Upload/2019/05/12/08/1a8f9afd/SYS201905120854095644903087_ST/SYS201905120854095644903087_ST.023.png" width="24" height="19" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />向![]() 點(diǎn)運(yùn)動(dòng),其中一個(gè)動(dòng)點(diǎn)到達(dá)端點(diǎn)時(shí),另一個(gè)也隨之停止運(yùn)動(dòng).設(shè)運(yùn)動(dòng)時(shí)間為
點(diǎn)運(yùn)動(dòng),其中一個(gè)動(dòng)點(diǎn)到達(dá)端點(diǎn)時(shí),另一個(gè)也隨之停止運(yùn)動(dòng).設(shè)運(yùn)動(dòng)時(shí)間為![]() 秒.
秒.
①當(dāng)![]() 為何值時(shí),四邊形
為何值時(shí),四邊形![]() 為等腰梯形;
為等腰梯形;
②設(shè)![]() 與對(duì)稱(chēng)軸的交點(diǎn)為
與對(duì)稱(chēng)軸的交點(diǎn)為![]() ,過(guò)
,過(guò)![]() 點(diǎn)作
點(diǎn)作![]() 軸的平行線(xiàn)交
軸的平行線(xiàn)交![]() 于點(diǎn)
于點(diǎn)![]() ,設(shè)四邊形
,設(shè)四邊形![]() 的面積為
的面積為![]() ,求面積
,求面積![]() 關(guān)于時(shí)間
關(guān)于時(shí)間![]() 的函數(shù)解析式,并指出
的函數(shù)解析式,并指出![]() 的取值范圍;當(dāng)
的取值范圍;當(dāng)![]() 為何值時(shí),
為何值時(shí),![]() 有最大值或最小值.
有最大值或最小值.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,我省在修建泛亞鐵路時(shí)遇到一座山,要從![]() 地向
地向![]() 地修一條隧道(
地修一條隧道(![]() ,
,![]() 在同一水平面上),為了測(cè)量
在同一水平面上),為了測(cè)量![]() ,
,![]() 兩地之間的距離,某工程師乘坐熱氣球從
兩地之間的距離,某工程師乘坐熱氣球從![]() 地出發(fā)垂直上升
地出發(fā)垂直上升![]() 米到達(dá)
米到達(dá)![]() 處,在
處,在![]() 處觀察
處觀察![]() 地的俯角為
地的俯角為![]() ,然后保持同一高度向前平移
,然后保持同一高度向前平移![]() 米到達(dá)
米到達(dá)![]() 處,在
處,在![]() 處觀察
處觀察![]() 地的俯角為
地的俯角為![]() ,則
,則![]() 、
、![]() 兩地之間的距離為多少米?(參考數(shù)據(jù):
兩地之間的距離為多少米?(參考數(shù)據(jù):![]() ;結(jié)果保留整數(shù))
;結(jié)果保留整數(shù))

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知m,n(m<n)是關(guān)于x的方程(x–a)(x–b)=2的兩根,若a<b,則下列判斷正確的是
A. a<m<b<n B. m<a<n<b
C. a<m<n<d D. m<a<b<n
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,小黃站在河岸上的![]() 點(diǎn),看見(jiàn)河里有一小船沿垂直于岸邊的方向劃過(guò)來(lái).此時(shí),測(cè)得小船
點(diǎn),看見(jiàn)河里有一小船沿垂直于岸邊的方向劃過(guò)來(lái).此時(shí),測(cè)得小船![]() 的俯角是
的俯角是![]() ,若小黃的眼睛與地面的距離
,若小黃的眼睛與地面的距離![]() 是
是![]() 米,
米,![]() 米,
米,![]() 平行于
平行于![]() 所在的直線(xiàn),迎水坡
所在的直線(xiàn),迎水坡![]() 的坡度為
的坡度為![]() ,坡長(zhǎng)
,坡長(zhǎng)![]() 米,則此時(shí)小船
米,則此時(shí)小船![]() 到岸邊的距離
到岸邊的距離![]() 的長(zhǎng)為( )米.(
的長(zhǎng)為( )米.(![]() ,結(jié)果保留兩位有效數(shù)字)
,結(jié)果保留兩位有效數(shù)字)

A. 11 B. 8.5 C. 7.2 D. 10
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】越來(lái)越多的人用微信聊天、轉(zhuǎn)賬、付款等.把微信賬戶(hù)里的錢(qián)轉(zhuǎn)到銀行卡叫做提現(xiàn).自2016年3月1日起,每個(gè)微信賬戶(hù)有1000元的免費(fèi)提現(xiàn)額度,當(dāng)累計(jì)提現(xiàn)超過(guò)這個(gè)額度時(shí),超出的部分需要付0.1%的手續(xù)費(fèi).
(1)小明的媽媽從未提現(xiàn)過(guò),此時(shí)想把微信零錢(qián)里的15000元提現(xiàn),那么將收取手續(xù)費(fèi) 元;
(2)小亮自2016年3月1日至今,用自己的微信賬戶(hù)共提現(xiàn)3次,3次提現(xiàn)金額和手續(xù)費(fèi)分別如下:
第一次提現(xiàn) | 第二次提現(xiàn) | 第三次提現(xiàn) | |
提現(xiàn)金額(元) | a | b | 3a+2b |
手續(xù)費(fèi)(元) | 0 | 0.4 | 3.4 |
①二元一次方程組的相關(guān)知識(shí)求表中a、b的值;
②小明3次提現(xiàn)金額共計(jì) 元.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com