
【題目】已知圓O的半徑長為2,點A、B、C為圓O上三點,弦BC=AO,點D為BC的中點,
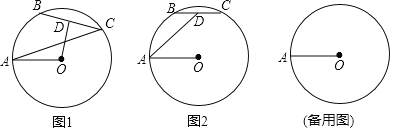
(1)如圖,連接AC、OD,設∠OAC=α,請用α表示∠AOD;
(2)如圖,當點B為![]() 的中點時,求點A、D之間的距離:
的中點時,求點A、D之間的距離:
(3)如果AD的延長線與圓O交于點E,以O為圓心,AD為半徑的圓與以BC為直徑的圓相切,求弦AE的長.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)連接OB、OC,可證△OBC是等邊三角形,根據垂徑定理可得∠DOC等于30°,OA=OC可得∠ACO=∠CAO=α,利用三角形的內角和定理即可表示出∠AOD的值.
(2)連接OB、OC,可證△OBC是等邊三角形,根據垂徑定理可得∠DOB等于30°,因為點D為BC的中點,則∠AOB=∠BOC=60°,所以∠AOD等于90°,根據OA=OB=2,在直角三角形中用三角函數及勾股定理即可求得OD、AD的長.
(3)分兩種情況討論:兩圓外切,兩圓內切.先根據兩圓相切時圓心距與兩圓半徑的關系,求出AD的長,再過O點作AE的垂線,利用勾股定理列出方程即可求解.
(1)如圖1:連接OB、OC.
∵BC=AO
∴OB=OC=BC
∴△OBC是等邊三角形
∴∠BOC=60°
∵點D是BC的中點
∴∠BOD=![]()
∵OA=OC
∴![]() =α
=α
∴∠AOD=180°-α-α-![]() =150°-2α
=150°-2α
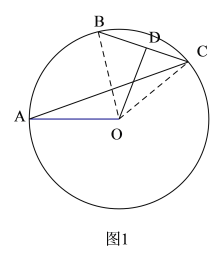
(2)如圖2:連接OB、OC、OD.
由(1)可得:△OBC是等邊三角形,∠BOD=![]()
∵OB=2,
∴OD=OBcos![]() =
=![]()
∵B為![]() 的中點,
的中點,
∴∠AOB=∠BOC=60°
∴∠AOD=90°
根據勾股定理得:AD=![]()
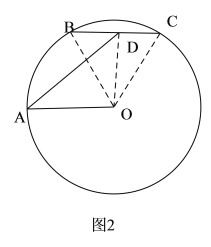
(3)①如圖3.圓O與圓D相內切時:
連接OB、OC,過O點作OF⊥AE
∵BC是直徑,D是BC的中點
∴以BC為直徑的圓的圓心為D點
由(2)可得:OD=![]() ,圓D的半徑為1
,圓D的半徑為1
∴AD=![]()
設AF=x
在Rt△AFO和Rt△DOF中,
![]()
即![]()
解得:![]()
∴AE=![]()

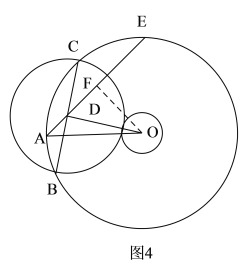
②如圖4.圓O與圓D相外切時:
連接OB、OC,過O點作OF⊥AE
∵BC是直徑,D是BC的中點
∴以BC為直徑的圓的圓心為D點
由(2)可得:OD=![]() ,圓D的半徑為1
,圓D的半徑為1
∴AD=![]()
在Rt△AFO和Rt△DOF中,
![]()
即![]()
解得:![]()
∴AE=![]()


 小天才課時作業系列答案
小天才課時作業系列答案 一課四練系列答案
一課四練系列答案 黃岡小狀元滿分沖刺微測驗系列答案
黃岡小狀元滿分沖刺微測驗系列答案 新輔教導學系列答案
新輔教導學系列答案科目:初中數學 來源: 題型:
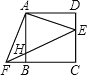
【題目】如圖,△ADE繞正方形ABCD的頂點A順時針旋轉90°,得△ABF,連接EF交AB于H,則下列結論: ①AE⊥AF;②EF:AF=![]() :1;③AF2=FHFE;④FB:FC=HB:EC.正確的是___.
:1;③AF2=FHFE;④FB:FC=HB:EC.正確的是___.
查看答案和解析>>
科目:初中數學 來源: 題型:
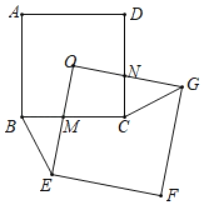
【題目】如圖,已知正方形OEFG的頂點O與正方形ABCD的中心O重合,若正方形OEFG繞O點旋轉.
(1)探究:在旋轉的過程中線段BE與線段CG有什么數量關系及位置關系?證明你的結論;
(2)若正方形ABCD的邊長為a,探究:在旋轉過程中四邊形OMCN的面積是否發生變化?若不變化求其面積,若變化指出變化過程.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在奉賢創建文明城區的活動中,有兩段長度相等的彩色道磚鋪設任務,分別交給甲、乙兩個施工隊同時進行施工.如圖是反映所鋪設彩色道磚的長度y(米)與施工時間x(時)之間關系的部分圖象.請解答下列問題:
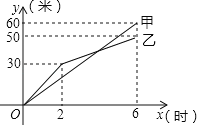
(1)求乙隊在2≤x≤6的時段內,y與x之間的函數關系式;
(2)如果甲隊施工速度不變,乙隊在開挖6小時后,施工速度增加到12米/時,結果兩隊同時完成了任務.求甲隊從開始施工到完工所鋪設的彩色道磚的長度為多少米?
查看答案和解析>>
科目:初中數學 來源: 題型:
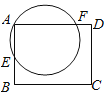
【題目】如圖,在矩形ABCD中,過點A的圓O交邊AB于點E,交邊AD于點F,已知AD=5,AE=2,AF=4.如果以點D為圓心,r為半徑的圓D與圓O有兩個公共點,那么r的取值范圍是______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,△ABC的三個頂點坐標分別為A(1,1),B(4,0),C(4,4).
(1)按下列要求作圖:
①將△ABC向左平移4個單位,得到△A1B1C1;
②將△A1B1C1繞點B1逆時針旋轉90°,得到△A2B2C2.
(2)求點C1在旋轉過程中所經過的路徑長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知點A(﹣3,y1),B(2,y2)均在拋物線y=ax2+bx+c上,點P(m,n)是該拋物線的頂點,若y1>y2≥n,則m的取值范圍是( )
A.﹣3<m<2B.﹣![]() <m<-
<m<-![]() C.m>﹣
C.m>﹣![]() D.m>2
D.m>2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,從一架水平飛行的無人機![]() 的尾端點
的尾端點![]() 測得正前方的橋的左端點
測得正前方的橋的左端點![]() 俯角為
俯角為![]() ,且
,且![]() ,無人機的飛行高度
,無人機的飛行高度![]() 米,橋的長度
米,橋的長度![]() 為1255米.
為1255米.
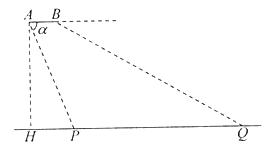
(1)求點![]() 到橋左端點
到橋左端點![]() 的距離;
的距離;
(2)若從無人機前端點![]() 測得正前方的橋的右端點
測得正前方的橋的右端點![]() 的俯角為
的俯角為![]() ,求這架無人機的長度
,求這架無人機的長度![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“長跑”是中考體育必考項目之一,鄧州市某中學為了了解九年級學生“長跑”的情況,隨機抽取部分九年級學生測試成績(男子1000米,女子800米),按長跑時間長短依次分為A,B,C,D四個等級進行統計,制作出如下兩個不完整的統計圖,根據所給信息,解答以下問題:
(1)在扇形統計圖中,C對應的扇形圓心角是 度;
(2)補全條形統計圖;
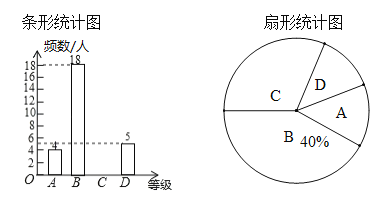
(3)所抽取學生的“長跑”測試成績的中位數會落在 等級;
(4)該校九年級有675名學生,請估計“長跑”測試成績達到A級的學生有多少人?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com