
【題目】如圖,已知,AB是⊙O的直徑,點P在AB的延長線上,弦CE交AB于點,連結OE,AC,且∠P=∠E,∠POE=2∠CAB.
(1)求證:CE⊥AB;
(2)求證:PC是⊙O的切線;
(3)若BD=2OD,且PB=9,求⊙O的半徑長和tan∠P的值.

【答案】(1)證明見解析;(2)證明見解析;(3)![]()
【解析】分析:(1)連結OC,如圖,根據圓周角定理得∠POC=2∠CAB,由于∠POE=2∠CAB,則∠POC=∠POE,根據等腰三角形的性質即可得到CE⊥AB;
(2)由CE⊥AB得∠P+∠PCE=90°,加上∠E=∠OCD,∠P=∠E,所以∠OCD+∠PCE=90°,則OC⊥PC,然后根據切線的判定定理即可得到結論.
(3)設⊙O的半徑為r,OD=x,則BD=2x,r=3x,易證得Rt△OCD∽Rt△OPC,根據相似三角形的性質得OC2=ODOP,即(3x)2=x(3x+9),解出x,即可得圓的半徑;同理可得PC2=PDPO=(PB+BD)(PB+OB)=162,可計算出PC,然后在Rt△OCP中,根據正切的定義即可得到tan∠P的值.
詳解:(1)證明:連接OC,

∴∠COB=2∠CAB,
又∠POE=2∠CAB.
∴∠COD=∠EOD,
又∵OC=OE,
∴∠ODC=∠ODE=90°,
即CE⊥AB;
(2)證明:∵CE⊥AB,∠P=∠E,
∴∠P+∠PCD=∠E+∠PCD=90°,
又∠OCD=∠E,
∴∠OCD+∠PCD=∠PCO=90°,
∴PC是⊙O的切線;
(3)解:設⊙O的半徑為r,OD=x,則BD=2x,r=3x,
∵CD⊥OP,OC⊥PC,
∴Rt△OCD∽Rt△OPC,
∴OC2=ODOP,即(3x)2=x(3x+9),
解之得x=![]() ,
,
∴⊙O的半徑r=![]() ,
,
同理可得PC2=PDPO=(PB+BD)(PB+OB)=162,
∴PC=9![]() ,
,
在Rt△OCP中,tan∠P=![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】計算:
(1)![]() -(+3.7)+(+
-(+3.7)+(+![]() )-(-1.7) (2)(-72)×2
)-(-1.7) (2)(-72)×2![]() ×(-
×(-![]() )÷(-3
)÷(-3![]() )
)
(3)(![]() -
-![]() -
-![]() +
+![]() )×(-24) (4)-32×(-2)+42÷(-2)3-∣-22∣
)×(-24) (4)-32×(-2)+42÷(-2)3-∣-22∣
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法,其中正確的個數是( )
①整數和分數統稱為有理數;②絕對值是它本身的數只有0;③兩數之和一定大于每個加數;④如果兩個數積為0,那么至少有一個因數為0;⑤0是最小的有理數,;⑥數軸上表示互為相反數的點位于原點的兩側;⑦幾個有理數相乘,如果負因數的個數是奇數,那么積為負數,
A.5個B.4個C.3個D.2個
查看答案和解析>>
科目:初中數學 來源: 題型:
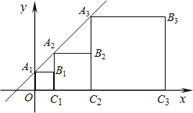
【題目】如圖,在直角坐標系中,正方形A1B1C1O、 A2B2C2C1、A3B3C3C2、…、AnBnCnCn-1的頂點A1、A2、A3、…、An均在直線y=kx+b上,頂點C1、C2、C3、…、Cn在x軸上,若點B1的坐標為(1,1),點B2的坐標為(3,2),那么點A4的坐標為 ,點An的坐標為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,ABCD中,AB=2cm,AC=5cm,SABCD=8cm2,E點從B點出發,以1cm每秒的速度,在AB延長線上向右運動,同時,點F從D點出發,以同樣的速度在CD延長線上向左運動,運動時間為t秒.
(1)在運動過程中,四邊形AECF的形狀是____;
(2)t=____時,四邊形AECF是矩形;
(3)求當t等于多少時,四邊形AECF是菱形.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,二次函數y=ax2+bx+c的圖象與x軸交于A、B兩點,與y軸交于點C,且OB=OC,下列結論:①b>1且b≠2;②b2﹣4ac<4a2;③a>![]() ;其中正確的個數為( )
;其中正確的個數為( )

A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,將一個圓依次二等分、三等分、四等分、五等分…,并按圖中規律在半徑上擺放黑色棋子,則第一幅圖中有5個棋子,第二幅圖中有10個棋子,第三幅圖中有17個棋子,第四幅圖中有26個棋子,依此規律,則第6幅圖中所含棋子數目為( )

A.51 B.50 C.49 D.48
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com