Question

（本小題滿分14分）

如圖①，已知四邊形ABCD是正方形，點E是AB的中點，點F在邊CB的延長線上，且BE=BF，連接EF．

1.（1）若取AE的中點P，求證：BP=CF；

2.（2）在圖①中，若將繞點B順時針方向旋轉（0⁰<<360⁰），如圖②，是否存在某位置，使得？，若存在，求出所有可能的旋轉角的大小；若不存在，請說明理由；

3.（3）在圖①中，若將△BEF繞點B順時針旋轉（0⁰<<90⁰），如圖③，取AE的中點P，連接BP、CF，求證：BP=CF且BP⊥CF．

 

Answer 1

 

1.解：（1）∵ AE = BE，AP = EP

∴ BE =2PE，AB = 4PE，BP = 3PE…………（1分）

∵ AB =BC，BE =BF      ∴ BC = 4PE，BF = 2PE

∴ CF =6PE…………（2分）        ∴

2.（2）存在…………（４分）

因為將繞點B順時針方向旋轉一周，E、F分別在以點B為圓心，BE為半徑的圓周上，如圖1，因此過Ａ點做圓Ｂ的切線，設切點是點Ｅ，此時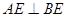，有AE∥BF。

當圓Ｂ的切線ＡＥ在ＡＢ的右側時，如圖1

∵ AE∥BF∴ ∠AEB = ∠EBF= 90°     ∵ BE = AB∴ ∠BAE = 30°

∴ ∠ABE = 60°，即旋轉角是60°…………（6分）

當圓Ｂ的切線ＡＥ在ＡＢ的左側時，如圖2

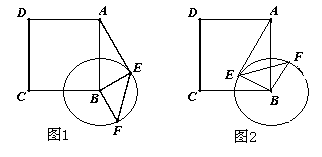如圖2，∵ AE∥BF

∴ ∠AEB + ∠EBF = 180°∴ ∠AEB = 90°

∵ BE = AB     ∴ ∠BAE = 30°

∴ ∠ABE = 60°，即旋轉角是300°

3.（3）延長BP到點G，使BP=PG，連結AG

∴ △APG ≌ △BPE

∴ AG =BE，PG = BP，∠G = ∠PBE

∵ BE =BF　　　∴ AG = BF

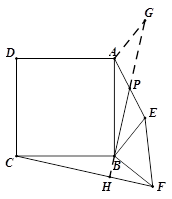∵ △BEF繞點B順時針旋轉   ∴ ∠ABE = ，∠CBF = 180°－

∵ ∠G = ∠PBE　　　　∴ ∠G + ∠ABP=

∴ ∠GAB = 180°－　　　∴ ∠GAB = ∠CBF

又∵ AB =BC，AG = BF

∴ △GAB ≌ △FBC　　　　∴BG = CF

∵ 　　　　∴ …………（11分）

延長PB，與CF相交于點H

∵ △GAB ≌ △FBC　　　　∴ ∠ABP = ∠BCH

∵ ∠ABP + ∠CBH = 90°　　　∴ ∠BCH + ∠CBH=90°

∴ BH⊥CF　　　　即 BP⊥CF…………（14分）

解析:略