【題目】已知：
，⊙
經過點
、
.以
為一邊畫平行四邊形
，另一邊
經過點（如圖1）.以點為圓心，
為半徑畫弧，交線段
于點
（點不與點、點
重合）.
（1）求證：
；
（2）如果⊙的半徑長為
（如圖2），設
，
，求
關于
的函數解析式，并寫出它的定義域；
（3）如果⊙的半徑長為，聯結
，當
時，求
的長.
【答案】（1）證明見解析；（2）
，得1分，函數定義域
，（3）3.
【解析】解決本題方法是根據題意添加輔助線，利用平行四邊形的性質和全等三角形性質解題即可.
解：（1）聯結
、
(如圖8-1)，
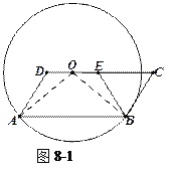
易得
，
.
∵四邊形
是平行四邊形，∴
∥
，
.
∵
，，∴
.
又 ∵∥，∴四邊形
是等腰梯形.∴
.
又 ∵，∴
.
即 
.
在△AOD和△BOE中，∵，，，
∴△AOD≌△BOE. ∴
.
方法2：∵
，
，，∴△AOD≌△BOE.……
方法3：∵
，，，∴△AOD≌△BOE.……
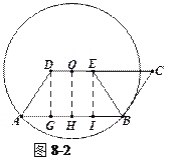
方法4：如圖8-2，過點
作
，過點
作
，過點
作
.……
方法5：如圖8-3，過點作，垂足為
，聯結
、
.……
（2）方法1：如圖9-1，
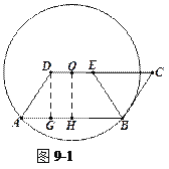
過點作，垂足為，過點作，垂足為
.
聯結，
，
，得1分；得到
，得2分；在Rt△ADG中，寫出
，
，得1分；利用
得到
，得1分，函數定義域，.
（3）如圖10-1，
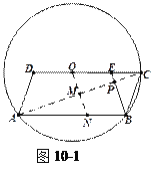
過點作
，交
于點
，交于點
.證明四邊形
是平行四邊形，利用
，
得到
，利用△AMN≌△CMO或
得到
，進而得到
是的垂直平分線，
，利用
，
得到
.
方法2.如圖10-2；方法3：如圖10-3；方法4（利用圓周角，略）.
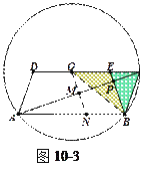
“點睛”本題考查了圓的綜合題：熟練掌握圓心角、弧、弦、弦心距之間的關系和三角形全等的判定與性質，也考查了分類討論的思想和勾股定理.本題時要注意一題多解的應用.
科目：初中數學 來源： 題型：
【題目】方程x2+2x﹣3=0的解是（ ）
A. x1=1，x2=3 B. x1=1，x2=﹣3
C. x1=﹣1，x2=3 D. x1=﹣1，x2=﹣3
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為“方便交通，綠色出行”，人們常選擇以共享單車作為代步工具、圖（1）所示的是一輛自行車的實物圖．圖（2）是這輛自行車的部分幾何示意圖，其中車架檔AC與CD的長分別為45cm和60cm，且它們互相垂直，座桿CE的長為20cm．點A、C、E在同一條直線上，且∠CAB=75°．
（參考數據：sin75°=0.966，cos75°=0.259，tan75°=3.732）
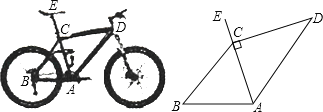
圖（1） 圖（2）
（1）求車架檔AD的長；
（2）求車座點E到車架檔AB的距離（結果精確到1cm）．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】△ABC中，∠A，∠B，∠C的對邊分別記為a，b，c，由下列條件不能判定△ABC為直角三角形的是（ ）
A. ∠A+∠B=∠C B. ∠A：∠B：∠C=1：2：3
C. a2=c2﹣b2 D. a：b：c=3：4：6
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
