
【題目】如圖,在平面直角坐標系中,點A、B的坐標分別為(﹣5,0)、(﹣2,0).點P在拋物線y=﹣2x2+4x+8上,設點P的橫坐標為m.當0≤m≤3時,△PAB的面積S的取值范圍是_____.

【答案】3≤S≤15.
【解析】
根據坐標先求AB的長,所以△PAB的面積S的大小取決于P的縱坐標的大小,因此只要討論當0≤m≤3時,P的縱坐標的最大值和最小值即可,根據頂點坐標D(1,4),由對稱性可知:x=1時,P的縱坐標最大,此時△PAB的面積S最大;當x=3時,P的縱坐標最小,此時△PAB的面積S最小.
∵點A、B的坐標分別為(-5,0)、(-2,0),
∴AB=3,
y=-2x2+4x+8=-2(x-1)2+10,
∴頂點D(1,10),
由圖象得:當0≤x≤1時,y隨x的增大而增大,
當1≤x≤3時,y隨x的增大而減小,
∴當x=3時,即m=3,P的縱坐標最小,
y=-2(3-1)2+10=2,
此時S△PAB=![]() ×2AB=
×2AB=![]() ×2×3=3,
×2×3=3,
當x=1時,即m=1,P的縱坐標最大是10,
此時S△PAB=![]() ×10AB=
×10AB=![]() ×10×3=15,
×10×3=15,
∴當0≤m≤3時,△PAB的面積S的取值范圍是3≤S≤15;
故答案為:3≤S≤15.


 考前必練系列答案
考前必練系列答案科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,BD平分∠ABC交AC于點D,AE∥BD交CB的延長線于點E.若∠E=35°,則∠BAC的度數為( )

A. 40° B. 45° C. 60° D. 70°
查看答案和解析>>
科目:初中數學 來源: 題型:
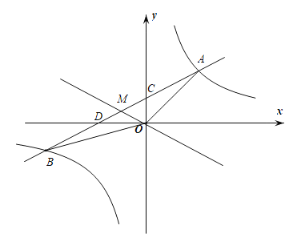
【題目】如圖,一次函數![]() 與反比例函數
與反比例函數![]() 相交于
相交于![]() 、
、![]() 兩點,與
兩點,與![]() 軸,
軸,![]() 軸分別交于
軸分別交于![]() 、
、![]() 兩點,已知
兩點,已知![]() ,
,![]() 的面積為
的面積為![]() .
.
(1)求一次函數和反比例函數的解析式;
(2)連接![]() ,
,![]() ,點
,點![]() 是線段
是線段![]() 的中點,直線
的中點,直線![]() 向上平移
向上平移![]() 個單位將
個單位將![]() 的面積分成
的面積分成![]() 兩部分,求
兩部分,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(10分)已知E,F分別為正方形ABCD的邊BC,CD上的點,AF,DE相交于點G,當E,F分別為邊BC,CD的中點時,有:①AF=DE;②AF⊥DE成立.
試探究下列問題:
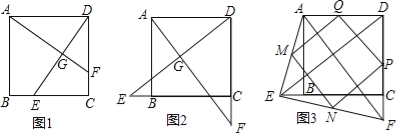
(1)如圖1,若點E不是邊BC的中點,F不是邊CD的中點,且CE=DF,上述結論①,②是否仍然成立?(請直接回答“成立”或“不成立”),不需要證明)
(2)如圖2,若點E,F分別在CB的延長線和DC的延長線上,且CE=DF,此時,上述結論①,②是否仍然成立?若成立,請寫出證明過程,若不成立,請說明理由;
(3)如圖3,在(2)的基礎上,連接AE和BF,若點M,N,P,Q分別為AE,EF,FD,AD的中點,請判斷四邊形MNPQ是“矩形、菱形、正方形”中的哪一種,并證明你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
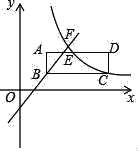
【題目】如圖,矩形ABCD在平面直角坐標系的第一象限內,BC與x軸平行,AB=1,點C的坐標為(6,2),E是AD的中點;反比例函數y1=![]() (x>0)圖象經過點C和點E,過點B的直線y2=ax+b與反比例函數圖象交于點F,點F的縱坐標為4.
(x>0)圖象經過點C和點E,過點B的直線y2=ax+b與反比例函數圖象交于點F,點F的縱坐標為4.
(1)求反比例函數的解析式和點E的坐標;
(2)求直線BF的解析式;
(3)直接寫出y1>y2時,自變量x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
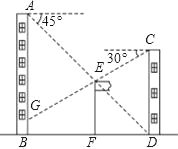
【題目】如圖,在樓AB與樓CD之間有一旗桿EF,從AB頂部A點處經過旗桿頂部E點恰好看到樓CD的底部D點,且俯角為45°,從樓CD頂部C點處經過旗桿頂部E點恰好看到樓AB的G點,BG=1米,且俯角為30°,已知樓AB高20米,求旗桿EF的高度.(結果精確到1米)
查看答案和解析>>
科目:初中數學 來源: 題型:
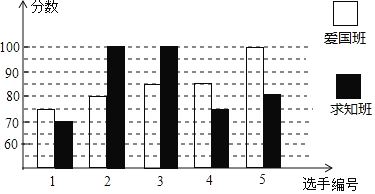
【題目】某校初二開展英語拼寫大賽,愛國班和求知班根據初賽成績,各選出5名選手參加復賽,兩個班各選出的5名選手的復賽成績如圖所示:
(1)根據圖示填寫下表:
班級 | 中位數(分) | 眾數(分) | 平均數(分) |
愛國班 | 85 | ||
求知班 | 100 | 85 |
(2)結合兩班復賽成績的平均數和中位數,分析哪個班級的復賽成績比較好?
(3)已知愛國班復賽成績的方差是70,請求出求知班復賽成績的方差,并說明哪個班成績比較穩定?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)發現規律:
特例1:![]() =
=![]() =
=![]() =
=![]() ;
;
特例2:![]() =
=![]() =
=![]() =
=![]() ;
;
特例3:![]() =4
=4![]() ;
;
特例4:______(填寫一個符合上述運算特征的例子);
(2)歸納猜想:
如果n為正整數,用含n的式子表示上述的運算規律為:______;
(3)證明猜想:
(4)應用規律:
①化簡:![]() ×
×![]() =______;
=______;
②若![]() =19
=19![]() ,(m,n均為正整數),則m+n的值為______.
,(m,n均為正整數),則m+n的值為______.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com