
【題目】如圖,△ABC內接于⊙O,∠B=60°,CD是⊙O的直徑,點P是CD延長線上的一點,且AP=AC.
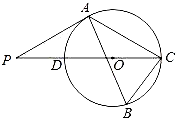
(1)求證:PA是⊙O的切線;
(2)若⊙O的半徑為3,求陰影部分的面積.
【答案】(1)證明見解析;(2)![]() .
.
【解析】
試題分析:(1)連接OA,如圖,先根據圓周角定理得到∠AOC=2∠B=120°,則∠AOP=60°,再計算出∠OCA的度數,接著利用AP=AC得到∠P=∠ACO=30°,然后根據三角形的內角和可計算出發∠APO=90°,于是利用切線的判定定理可判斷出PA是⊙O的切線;
(2)在Rt△AOP中,利用含30度的直角三角形三邊的關系得到PO=2OA=6,PA=![]() OA=3
OA=3![]() ,然后根據三角形面積公式和扇形面積公式進行計算即可.
,然后根據三角形面積公式和扇形面積公式進行計算即可.
試題解析:(1)連接OA,如圖,
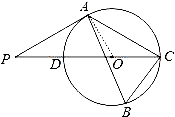
∵∠AOC=2∠B=120°,
∴∠AOP=60°,
∵OA=OC,
∴∠OCA=∠OAC=![]() (180°-120°)=30°,
(180°-120°)=30°,
∵AP=AC,
∴∠P=∠ACO=30°,
∴∠PAO=180°-30°-60°=90°,
∴OA⊥PA,
∴PA是⊙O的切線;
(2)在Rt△AOP中,PO=2OA=6,PA=![]() OA=3
OA=3![]() ,
,
∴S陰影部分=S△PAO-S扇形OAD=![]() .
.


 精英口算卡系列答案
精英口算卡系列答案科目:初中數學 來源: 題型:
【題目】下列描述一次函數y=﹣2x+5的圖象和性質錯誤的是( )
A.y隨x的增大而減小B.直線與x軸交點的坐標是(0,5)
C.當x>0時y<5D.直線經過第一、二、四象限
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法中正確的是( )
①圓心角是頂點在圓心的角;②兩個圓心角相等,它們所對的弦相等;③兩條弦相等,圓心到這兩弦的距離相等;④在等圓中,圓心角不變,所對的弦也不變.
A. ①③ B. ②④ C. ①④ D. ②③
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】汽車離開甲站10千米后,以60千米/時的速度勻速前進了t小時,則汽車離開甲站所走的路程s(千米)與時間t(小時)之間的關系式是( )
A.s=10+60t
B.s=60t
C.s=60t-10
D.s=10-60t
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如果△ABC∽△A′B′C′,BC=3,B′C′=1.8,則△A′B′C′與△ABC的相似比為( )
A.5∶3B.3∶2 C.2∶3D.3∶5
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com