
【題目】如圖,BE⊥AC于E,CF⊥AB于F,AE=AF,BE與CF交于點D,則:①△ABE≌△ACF;②△BDF≌△CDE;③點D在∠BAC的平分線上.以上結論正確的是( )
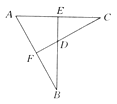
A. ① B. ② C. ①② D. ①②③
科目:初中數學 來源: 題型:
【題目】若十位上的數字比個位上的數字、百位上的數字都大的三位數叫做中高數,如796就是一個“中高數”.若一個三位數的十位上數字為7,且從4、5、6、8中隨機選取兩數,與7組成“中高數”,那么組成“中高數”的概率是多少?(請用“畫樹狀圖”或“列表”等方法寫出分析過程)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,在下列各圖中,點O為直線AB上一點,∠AOC=60°,直角三角板的直角頂點放在點處.
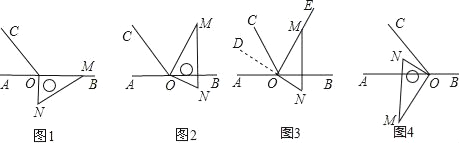
(1)如圖1,三角板一邊OM在射線OB上,另一邊ON在直線AB的下方,則∠BOC的度數為 °,∠CON的度數為 °;
(2)如圖2,三角板一邊OM恰好在∠BOC的角平分線OE上,另一邊ON在直線AB的下方,此時∠BON的度數為 °;
(3)請從下列(A),(B)兩題中任選一題作答.
我選擇: .
(A)在圖2中,延長線段NO得到射線OD,如圖3,則∠AOD的度數為 °;∠DOC與∠BON的數量關系是∠DOC ∠BON(填“>”、“=”或“<”);
(B)如圖4,MN⊥AB,ON在∠AOC的內部,若另一邊OM在直線AB的下方,則∠COM+∠AON的度數為 °;∠AOM﹣∠CON的度數為 °.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀后解決問題:
在“15.3分式方程”一課的學習中,老師提出這樣的一個問題:如果關于x的分式方程![]() 的解為正數,那么a的取值范圍是什么?
的解為正數,那么a的取值范圍是什么?
經過交流后,形成下面兩種不同的答案:
小明說:解這個關于x的分式方程,得到方程的解為x=a﹣2.
因為解是正數,可得a﹣2>0,所以a>2.
小強說:本題還要必須a≠3,所以a取值范圍是a>2且a≠3.
(1)小明與小強誰說的對,為什么?
(2)關于x的方程![]() 有整數解,求整數m的值.
有整數解,求整數m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一個底面直徑為 5cm,高為 18cm 的圓柱形瓶內裝滿水,再將瓶內得水倒入一個底面直徑為 6cm,高為 10cm 的圓柱形玻璃杯中,能否完全裝下? 若裝不下,那么瓶內水面還有多高? 若未能裝滿,求杯內水面離杯口的距離.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】蕪湖長江大橋是中國跨度最大的公路和鐵路兩用橋梁,大橋采用低塔斜拉橋橋型(如甲圖),圖乙是從圖甲引申出的平面圖,假設你站在橋上測得拉索AB與水平橋面的夾角是30°,拉索CD與水平橋面的夾角是60°,兩拉索頂端的距離BC為2米,兩拉索底端距離AD為20米,請求出立柱BH的長.(結果精確到0.1米, ![]() ≈1.732)
≈1.732)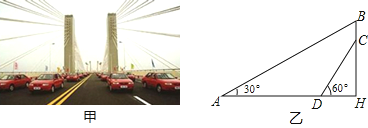
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將等腰△ABC繞頂點B逆時針方向旋轉α度到△A1B1C1的位置,AB與A1C1相交于點D,AC與A1C1、BC1分別交于點E、F.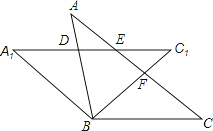
(1)求證:△BCF≌△BA1D.
(2)當∠C=α度時,判定四邊形A1BCE的形狀并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如果一個分式的分子或分母可以因式分解,且這個分式不可約分,那么我們稱這
個分式為“和諧分式”.
(1)下列分式:①![]() ;②
;②![]() ;③
;③![]() ;④
;④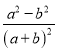 . 其中是“和諧分式”是 (填寫序號即可);
. 其中是“和諧分式”是 (填寫序號即可);
(2)若![]() 為正整數,且
為正整數,且![]() 為“和諧分式”,請寫出
為“和諧分式”,請寫出![]() 的值;
的值;
(3)在化簡![]() 時,
時,
小東和小強分別進行了如下三步變形:
小東: ![]()
![]()

小強: ![]()
![]()
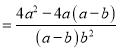
顯然,小強利用了其中的和諧分式, 第三步所得結果比小東的結果簡單,
原因是: ,
請你接著小強的方法完成化簡.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com