
【題目】如圖,已知拋物線![]() 的頂點坐標為
的頂點坐標為![]() ,且與
,且與![]() 軸交于點C
軸交于點C![]() ,與
,與![]() 軸交于A、B兩點(點A在點B的右側).
軸交于A、B兩點(點A在點B的右側).
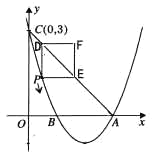
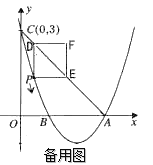
(1)求該拋物線的函數關系式;
(2)點P是該拋物線上一動點,從點C沿拋物線向點A運動(點P與A不重合),過點P作PD∥![]() 軸,交直線AC于點D;作PE∥x軸,交直線AC于點E,以PD,PE為邊的矩形PEFD,問矩形PEFD周長是否存在最大值?若存在,求出此時P點的坐標及最大值;若不存在,請說明理由;
軸,交直線AC于點D;作PE∥x軸,交直線AC于點E,以PD,PE為邊的矩形PEFD,問矩形PEFD周長是否存在最大值?若存在,求出此時P點的坐標及最大值;若不存在,請說明理由;
(3)在問題(2)的條件下,P點滿足∠DAP=90°,且點E在![]() 軸上,點F在拋物線上,問是否存在以A、P、E、F為頂點的平行四邊形?若存在,求點F的坐標;若不存在,請說明理由.
軸上,點F在拋物線上,問是否存在以A、P、E、F為頂點的平行四邊形?若存在,求點F的坐標;若不存在,請說明理由.
【答案】(1)y=x24x+3(2)存在,當P(![]() ,-
,-![]() ),矩形PEFD周長最大值為9(3)F1(2
),矩形PEFD周長最大值為9(3)F1(2![]() ,1),F2(2+
,1),F2(2+![]() ,1).
,1).
【解析】
(1)已知了拋物線的頂點坐標,可將拋物線的解析式設為頂點式,然后將函數圖象經過的C點坐標代入上式中,即可求出拋物線的解析式;
(2)先求出A點坐標,可知△AOC是等腰直角三角形,再求出直線AC的解析式,由題意可知矩形PEFD為正方形,故矩形PEFD周長等于4DP,設P(x, x24x+3),再表示出D點坐標及DP的長,根據二次函數的性質即可求出最大值;
(3)根據∠DAP=90°,過P點作AP⊥AC于拋物線的交點即為P點,根據平行四邊形的性質知:P、F的縱坐標互為相反數,可據此求出F點的縱坐標,代入拋物線的解析式中即可求出F點的坐標.
(1)∵拋物線的頂點為(2,1),
∴設拋物線的解析式為y=a(x2)21,
將C(0,3)代入上式,得:
3=a(02)21,a=1;
∴y=(x2)21,即y=x24x+3;
(2)令y=0,即x24x+3=0
解得x1=1,x2=3
∴A(3,0)
∴CO=AO
∴△AOC是等腰直角三角形,∠CAO=45°
設直線AC的解析式為y=kx+b(k≠0),
把A(3,0),C(0,3)代入得![]()
解得![]()
∴直線AC的解析式為y=-x+3
∵PE∥x軸,
∴∠DPE=∠CAO=45°
∴∠EDP=90°-∠DPE=45°
∴DP=PE
故矩形PEFD為正方形,
設P(x, x24x+3),則D(x,-x+3)
∴DP=(-x+3)-(x24x+3)=-x2+3x
∴矩形PEFD周長C=4DP=-4x2+12x=-4(x2-3x)= -4(x-![]() )2+9
)2+9
故存在當x=![]() 時,即P(
時,即P(![]() ,-
,-![]() ),矩形PEFD周長最大值為9;
),矩形PEFD周長最大值為9;
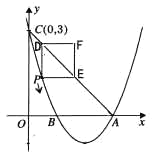
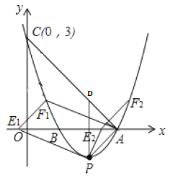
(3)如圖,過P點作AP⊥AC于拋物線的交點即為P點,此時∠DAP=90°,
∵直線AC的解析式為y=-x+3
∴可設直線AP的解析為y=x+p
把A(3,0)代入得0=3+p
解得p=-3
∴直線AP的解析為y=x-3
聯立![]()
解得x1=3,y=0或x=2,y=-1
∴P(2,-1)
∵A、P、E、F為頂點的平行四邊形
∴P、F的縱坐標互為相反數,
∴可設F(x,1),代入拋物線可得x24x+3=1,
解得x1=2![]() ,x2=2+
,x2=2+![]() ;
;
∴符合條件的F點有兩個,
即F1(2![]() ,1),F2(2+
,1),F2(2+![]() ,1).
,1).


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,矩形ABCD的頂點A、B、C的坐標分別為(0,5)(0,2)(4,2),直線l的解析式為y = kx+5-4k(k > 0).
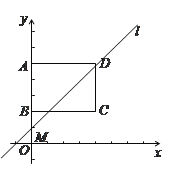
(1)當直線l經過點B時,求一次函數的解析式;
(2)通過計算說明:不論k為何值,直線l總經過點D;
(3)直線l與y軸交于點M,點N是線段DM上的一點, 且△NBD為等腰三角形,試探究:
①當函數y = kx+5-4k為正比例函數時,點N的個數有 個;
②點M在不同位置時,k的取值會相應變化,點N的個數情況可能會改變,請直接寫出點N所有不同的個數情況以及相應的k的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1和圖2是兩張形狀和大小完全相同的方格紙,方格紙中每個小正方形的邊長均為1,線段AC的兩個端點均在小正方形的頂點上.
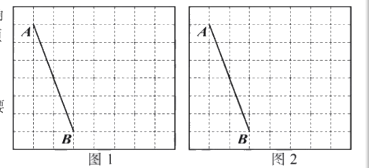
(1)在圖1中畫出以AB為斜邊的直角三角形ABC,點C在小正方形的頂點上,且![]() ;
;
(2)在圖2中畫出以AB為一邊的等腰三角形ABD,點D在小正方形的頂點上,且![]() 的面積為16.
的面積為16.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙二人均從A地出發,甲以60米/分的速度向東勻速行進,10分鐘后,乙以(60+m)米/分的速度按同樣的路線去追趕甲,乙出發5.5分鐘后,甲以原速原路返回,在途中與乙相遇,相遇后兩人均停止行進.設乙所用時間為t分鐘.
(1)當m=6時,解答:
①設甲與A地的距離為![]() ,分別求甲向東行進及返回過程中,
,分別求甲向東行進及返回過程中,![]() 與t的函數關系式(不寫t的取值范圍);
與t的函數關系式(不寫t的取值范圍);
②當甲、乙二人在途中相遇時,求甲行進的總時間.
(2)若乙在出發9分鐘內與甲相遇,求m的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,將正方形OABC繞點O逆時針旋轉45°后得到正方形![]() ,以此方式,繞點O旋轉2018次得到正方形
,以此方式,繞點O旋轉2018次得到正方形![]() ,如果點A的坐標為(1,0),那么那么點
,如果點A的坐標為(1,0),那么那么點![]() 的坐標為_____.
的坐標為_____.
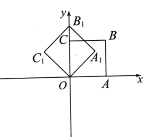
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解某校九年級學生的理化實驗操作情況,隨機抽查了40名同學實驗操作的得分,根據獲取的樣本數據,制作了如下的條形統計圖和扇形統計圖.請根據相關信息,解答下列問題:
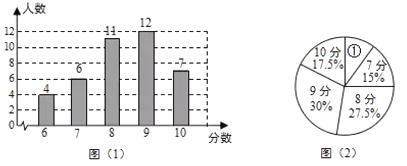
(1)①中的描述應為“6分![]() ”,其中
”,其中![]() 的值為 ;扇形①的圓心角的大小是 ;
的值為 ;扇形①的圓心角的大小是 ;
(2)求這40個樣本數據的平均數、眾數、中位數;
(3)若該校九年級共有360名學生,估計該校理化實驗操作得滿分的學生有多少人.
查看答案和解析>>
科目:初中數學 來源: 題型:
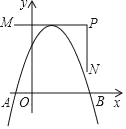
【題目】如圖,拋物線y=ax2+bx+c與x軸相交于A、B兩點,點A在點B左側,頂點在折線M﹣P﹣N上移動,它們的坐標分別為M(﹣1,4)、P(3,4)、N(3,1).若在拋物線移動過程中,點A橫坐標的最小值為﹣3,則a﹣b+c的最小值是_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】綜合與實踐
操作發現:
如圖1和圖2,已知點![]() 為正方形
為正方形![]() 的邊
的邊![]() 和
和![]() 上的一個動點(點
上的一個動點(點![]() ,
,![]() ,
,![]() 除外),作射線
除外),作射線![]() ,作
,作![]() 于點
于點![]() ,
,![]() 于點
于點![]() ,
,![]() 于點
于點![]() .
.
(1)如圖1,當點![]() 在
在![]() 上(點
上(點![]() ,
,![]() 除外)運動時,求證:
除外)運動時,求證:![]() ;
;
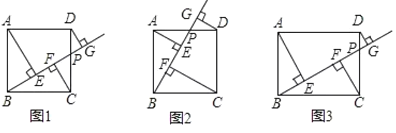
(2)如圖2,當點![]() 在
在![]() 上(點
上(點![]() ,
,![]() 除外)運動時,請直接寫出線段
除外)運動時,請直接寫出線段![]() ,
,![]() ,
,![]() 之間的數量關系;
之間的數量關系;
拓廣探索:
(3)在(1)的條件下,找出與![]() 相等的線段,并說明理由;
相等的線段,并說明理由;
(4)如圖3,若點![]() 為矩形
為矩形![]() 的邊
的邊![]() 上一點,作射線
上一點,作射線![]() ,作
,作![]() 于點
于點![]() ,
,![]() 于點
于點![]() ,
,![]() 于點
于點![]() .若
.若![]()
![]() ,
,![]() ,則
,則![]() _______.
_______.
查看答案和解析>>
科目:初中數學 來源: 題型:
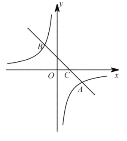
【題目】如圖,在平面直角坐標系中,一次函數![]() 的圖像與反比例函數
的圖像與反比例函數![]() 的圖像交與A(4,-2),B(-2,n)兩點,與
的圖像交與A(4,-2),B(-2,n)兩點,與![]() 軸交與點C.
軸交與點C.
(1)求![]() ,n的值;
,n的值;
(2)請直接寫出不等式![]() 的解集;
的解集;
(3)點A關于![]() 軸對稱得到點A’,連接A’B,A’C,求△A’BC的面積.
軸對稱得到點A’,連接A’B,A’C,求△A’BC的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com