【題目】甲、乙兩超市(大型商場)同時開業，為了吸引顧客，都舉行了有獎酬賓活動：凡購物滿100元，均可得到一次摸獎的機會. 在一個紙盒里裝有2個紅求和2個白球，除顏色外其他都相同，摸獎者一次從中摸出兩個球，根據球的顏色決定送禮金券(在他們超市使用時，與人民幣等值)的多少（如下表）
甲 超 市
球 | 兩紅 | 一紅一白 | 兩白 |
禮金券 | 5 | 10 | 5 |
乙 超 市
球 | 兩紅 | 一紅一白 | 兩白 |
禮金券 | 10 | 5 | 10 |
（1）用樹狀圖或列表法表示得到一次摸獎機會時中禮金券的所有情況；
（2）如果只考慮中獎因素，你將會選擇去哪個超市購物？請說明理由.
【答案】（1）答案見解析；（2）我選擇去甲超市購物，理由見解析.
【解析】（1）讓所求的情況數除以總情況數即為所求的概率；
（2）算出相應的平均收益，比較即可．
解：（1）樹狀圖：
（2）方法1：∵去甲超市購物摸一次獎獲10元禮金券的概率P(甲)= 
= 
,
去乙超市購物摸一次獎獲10元禮金券的概率P(乙)= 
=
,
∴P(甲)> P(乙) ∴我選擇去甲超市購物
方法2：∵P(兩紅)= 
,P(兩白)= 
,P(一紅一白)= 
,
∴在甲商場獲禮金券的平均收益是
×5+
×10+
×5=
,
在乙商場獲禮金券的平均收益是
×10+
×5+
×10=
,
∴
>
,∴我選擇去甲超市購物
“點睛”樹狀圖法適合兩步或兩步以上完成的事件；解題時要注意此題是放回實驗還是不放回實驗．用到的知識點為：概率=所求情況數與總情況數之比．
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，點A的坐標為（0，4），△OAB沿x軸向右平移后得到△O′A′B′，點A的對應點A′是直線y= 
x上一點，則點B與其對應點B′間的距離為 ． 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，△ABC中，∠C=90°，邊AB的垂直平分線交AB、AC邊分別為點D，點E，連結BE．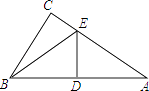 
（1）若∠A=40°，求∠CBE的度數．
（2）若AB=10，BC=6，求△BCE的周長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在Rt△ABC中，∠ACB=90°，AB=5，AC=3，點D是BC上一動點，連結AD，將△ACD沿AD折疊，點C落在點C′，連結C′D交AB于點E，連結BC′．當△BC′D是直角三角形時，DE的長為_____．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知空氣的密度是1.293 kg/m3，現有一只塑料袋內裝滿了空氣，其體積為0.0035 cm3，那么這一袋空氣的質量約為多少千克？(質量＝密度×體積，結果用科學記數法表示)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com