
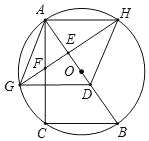
【題目】如圖,Rt△ABC,CA⊥BC,AC=4,在AB邊上取一點D,使AD=BC,作AD的垂直平分線,交AC邊于點F,交以AB為直徑的⊙O于G,H,設BC=x.
(1)求證:四邊形AGDH為菱形;
(2)若EF=y,求y關于x的函數關系式;
(3)連結OF,CG.
①若△AOF為等腰三角形,求⊙O的面積;
②若BC=3,則![]() CG+9=______.(直接寫出答案).
CG+9=______.(直接寫出答案).
【答案】(1)證明見解析;(2)y=![]() x2(x>0);(3)①
x2(x>0);(3)①![]() π或8π或(2
π或8π或(2![]() +2)π;②4
+2)π;②4![]() .
.
【解析】
(1)根據線段的垂直平分線的性質以及垂徑定理證明AG=DG=DH=AH即可;
(2)只要證明△AEF∽△ACB,可得![]() 解決問題;
解決問題;
(3)①分三種情形分別求解即可解決問題;
②只要證明△CFG∽△HFA,可得![]() =
=![]() ,求出相應的線段即可解決問題;
,求出相應的線段即可解決問題;
(1)證明:∵GH垂直平分線段AD,
∴HA=HD,GA=GD,
∵AB是直徑,AB⊥GH,
∴EG=EH,
∴DG=DH,
∴AG=DG=DH=AH,
∴四邊形AGDH是菱形.
(2)解:∵AB是直徑,
∴∠ACB=90°,
∵AE⊥EF,
∴∠AEF=∠ACB=90°,
∵∠EAF=∠CAB,
∴△AEF∽△ACB,
∴![]() ,
,
∴![]() ,
,
∴y=![]() x2(x>0).
x2(x>0).
(3)①解:如圖1中,連接DF.
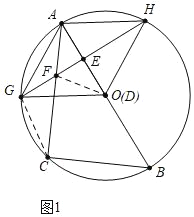
∵GH垂直平分線段AD,
∴FA=FD,
∴當點D與O重合時,△AOF是等腰三角形,此時AB=2BC,∠CAB=30°,
∴AB=![]() ,
,
∴⊙O的面積為![]() π.
π.
如圖2中,當AF=AO時,
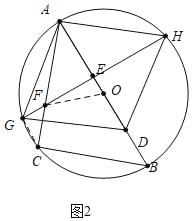
∵AB=![]() =
=![]() ,
,
∴OA=![]() ,
,
∵AF=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
解得x=4(負根已經舍棄),
∴AB=![]() ,
,
∴⊙O的面積為8π.
如圖2﹣1中,當點C與點F重合時,設AE=x,則BC=AD=2x,AB=![]() ,
,
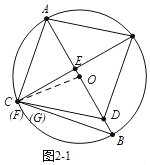
∵△ACE∽△ABC,
∴AC2=AEAB,
∴16=x![]() ,
,
解得x2=2![]() ﹣2(負根已經舍棄),
﹣2(負根已經舍棄),
∴AB2=16+4x2=8![]() +8,
+8,
∴⊙O的面積=π![]() AB2=(2
AB2=(2![]() +2)π
+2)π
綜上所述,滿足條件的⊙O的面積為![]() π或8π或(2
π或8π或(2![]() +2)π;
+2)π;
②如圖3中,連接CG.
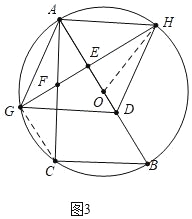
∵AC=4,BC=3,∠ACB=90°,
∴AB=5,
∴OH=OA=![]() ,
,
∴AE=![]() ,
,
∴OE=OA﹣AE=1,
∴EG=EH=![]() =
=![]() ,
,
∵EF=![]() x2=
x2=![]() ,
,
∴FG=![]() ﹣
﹣![]() ,AF=
,AF=![]() =
=![]() ,AH=
,AH=![]() =
=![]() ,
,
∵∠CFG=∠AFH,∠FCG=∠AHF,
∴△CFG∽△HFA,
∴![]() ,
,
∴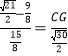 ,
,
∴CG=![]() ﹣
﹣![]() ,
,
∴![]() CG+9=4
CG+9=4![]() .
.
故答案為4![]() .
.


科目:初中數學 來源: 題型:
【題目】某景區商店以2元的批發價進了一批紀念品.經調查發現,每個定價3元,每天可以能賣出500件,而且定價每上漲0.1元,其銷售量將減少10件.根據規定:紀念品售價不能超過批發價的2.5倍.
(1)當每個紀念品定價為3.5元時,商店每天能賣出________件;
(2)如果商店要實現每天800元的銷售利潤,那該如何定價?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數圖象的對稱軸是x+3=0,圖象經過(1,﹣6),且與y軸的交點為(0,![]() ).
).
(1)求這個二次函數的解析式;
(2)當x為何值時,這個函數的函數值為0;
(3)當x在什么范圍內變化時,這個函數的函數值y隨x的增大而增大?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,∠ACB=90°,sinA=![]() ,BC=8,點D是AB的中點,過點B作CD的垂線,垂足為點E.
,BC=8,點D是AB的中點,過點B作CD的垂線,垂足為點E.
(1)求線段CD的長;
(2)求cos∠ABE的值。

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:二次函數圖象的頂點坐標是(3,5),且拋物線經過點A(1,3).
(1)求此拋物線的表達式;
(2)如果點A關于該拋物線對稱軸的對稱點是B點,且拋物線與y軸的交點是C點,求△ABC的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
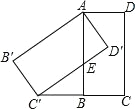
【題目】如圖,將矩形ABCD繞點A順時針旋轉,得到矩形AB′C′D′,點 C的對應點 C′恰好落在CB的延長線上,邊AB交邊 C′D′于點E.
(1)求證:BC=BC′;
(2)若 AB=2,BC=1,求AE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在一次測繪活動中,某同學站在點A處觀測停放于B、C兩處的小船,測得船B在點A北偏東75°方向150米處,船C在點A南偏東15°方向120米處,則船B與船C之間的距離為______米(精確到0.1![]() ).
).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“五一勞動節大酬賓!”,某商場設計的促銷活動如下:在一個不透明的箱子里放有4個相同的小球,球上分別標有“0元”、“10元”、“20元”和“50元”的字樣.規定:在本商場同一日內,顧客每消費滿300元,就可以在箱子里先后摸出兩個球(第一次摸出后不放回).商場根據兩小球所標金額的和返還相等價格的購物券,購物券可以在本商場消費.某顧客剛好消費300元.
(1)該顧客至多可得到________元購物券;
(2)請你用畫樹狀圖或列表的方法,求出該顧客所獲得購物券的金額不低于50元的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖AB是半圓的直徑,圖1中,點C在半圓外;圖2中,點C在半圓內,請僅用無刻度的直尺按要求畫圖.
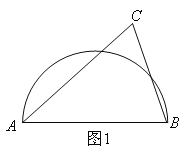
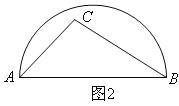
(1)在圖1中,畫出△ABC的三條高的交點;
(2)在圖2中,畫出△ABC中AB邊上的高.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com