
【題目】如圖,一次函數![]() 的圖像與反比例函數
的圖像與反比例函數![]() 的圖像交于點A﹙2,4﹚、C﹙4,n﹚,交y軸于點B,交x軸于點D.
的圖像交于點A﹙2,4﹚、C﹙4,n﹚,交y軸于點B,交x軸于點D.
(1)求反比例函數![]() 和一次函數
和一次函數![]() 的表達式;
的表達式;
(2)連接OA、OC,求△AOC的面積;
(3)寫出使一次函數的值大于反比例函數的![]() 的取值范圍 .
的取值范圍 .

【答案】(1)![]() ;(2)6;(3)-2<x<0或x>4
;(2)6;(3)-2<x<0或x>4
【解析】
(1)把點A(-2,-4)代入反比例函數的解析式,求出m的值,得到反比例函數不含m的解析式,把點C(4,n)代入反比例函數解析式,求出n的值,從而得到點C的坐標,用待定系數法求出一次函數的表達式即可;
(2)根據(1)求得的反比例函數求得點B和點D的坐標,將△AOC看作△AOB,△BOD的面積和△COD的和,分別計算面積,再求和,即可得到答案;
(3)根據函數圖象,寫出當x值相同時,一次函數的值大于反比例函數的值的x的取值范圍即可.
解:(1)把點A(-2,-4)代入反比例函數的解析式![]() 得:-4=
得:-4=![]() ,
,
解得:m=10,
即反比例函數的解析式為:y=![]() ,
,
把點C(4,n)代入解析式y=![]() 得:n=2,
得:n=2,
∴點C的坐標為(4,2),
把點A(-2,-4)和點C(4,2)代入y=kx+b得:
![]() ,
,
解得:
![]() ,
,
∴一次函數的表達式為y=x-2;
(2)把x=0代入y=x-2得:y=-2,
即OB=2,
把y=0代入y=x-2得:x=2,
即OD=2,
∵A(-2,-4),C(4,2),
∴點A到y軸的距離為2,點C到x軸的距離為2,
∴△AOB的面積=![]() ×2×2=2,
×2×2=2,
△BOD的面積=![]() ×2×2=2,
×2×2=2,
△COD的面積=![]() ×2×2=2,
×2×2=2,
△AOC的面積=△AOB的面積+△BOD的面積+△COD的面積=6,
即AOC的面積為6;
(3)通過觀察圖象可知:
使一次函數的值大于反比例函數的x的取值范圍為:-2<x<0或x>4.


 開心蛙狀元作業系列答案
開心蛙狀元作業系列答案 課時掌控隨堂練習系列答案
課時掌控隨堂練習系列答案 一課一練一本通系列答案
一課一練一本通系列答案科目:初中數學 來源: 題型:
【題目】填寫證明的理由:
已知,如圖AB∥CD,EF、CG分別是∠ABC、∠ECD的角平分線.
求證:EF∥CG
證明:∵AB∥CD(已知)
∴∠AEC=∠ECD( )
又EF平分∠AEC、CG平分∠ECD(已知)
∴∠1=![]() ∠ ,∠2=
∠ ,∠2=![]() ∠ (角平分線的定義)
∠ (角平分線的定義)
∴∠1=∠2( )
∴EF∥CG( )

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,Rt△ABC中,AC=BC=2,正方形CDEF的頂點D、F分別在AC、BC邊上,C、D兩點不重合,設CD的長度為x,△ABC與正方形CDEF重疊部分的面積為y,則下列圖象中能表示y與x之間的函數關系的是( )


A. (A) B. (B) C. (C) D. (D)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列圖案由邊長相等的黑,白兩色正方形按一定規律拼接而成,設第![]() 個圖案中白色小正方形的個數為
個圖案中白色小正方形的個數為![]() .
.
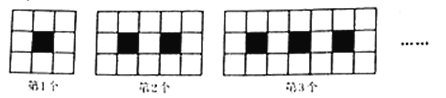
(1)第2個圖案中有______個白色的小正方形;第3個圖案中有______個白色的小正方形;![]() 與
與![]() 之間的函數表達式為______(直接寫出結果).
之間的函數表達式為______(直接寫出結果).
(2)是否存在這樣的圖案,使白色小正方形的個數為2019個?如果存在,請指出是第幾個圖案;如果不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知在Rt△ABC中,∠ACB=90°,AC > BC,CD是Rt△ABC的高,E是AC的中點,ED的延長線與CB的延長線相交于點F.
(1)求證:DF是BF和CF的比例中項;
(2)在AB上取一點G,如果AE·AC=AG·AD,求證:EG·CF=ED·DF.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明同學要測量學校的國旗桿BD的高度.如圖,學校的國旗桿與教學樓之間的距AB=20m.小明在教學樓三層的窗口C測得國旗桿頂點D的仰角為14°,旗桿底部B的俯角為22°.
(1)求∠BCD的大小.
(2)求國旗桿BD的高度(結果精確到1m.參考數據:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,sin14°≈0.24,cos14°≈0.97,tan14°≈0.25)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,已知![]() ,其中a,b滿足
,其中a,b滿足![]()

(1)填空:a= ,b= ;
(2)如果在第三象限內有一點C(-2,m),請用含m的式子表示△ABC的面積;
(3)在⑵條件下,當![]() 時,在y軸上有一點P,使得△BMP的面積與△ABM的面積相等,請求出點P的坐標.
時,在y軸上有一點P,使得△BMP的面積與△ABM的面積相等,請求出點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2019年2月14日,備受關注的《成都市中小學課后服務實施意見》正式出臺.某區為了解“家長更希望如何安排孩子放學后的時間”,對該區七年級部分家長進行了一次問卷調查(每位同學只選擇一位家長參與調查),將調查結果(![]() .回家,家人陪伴;
.回家,家人陪伴;![]() .學校課后延時服務;
.學校課后延時服務;![]() .校外培訓機構;
.校外培訓機構;![]() .社會托管班)繪制成以下兩幅不完整的統計圖.請根據圖中提供的信息,解答下列問題:
.社會托管班)繪制成以下兩幅不完整的統計圖.請根據圖中提供的信息,解答下列問題:

(1)本次調查的家長總人數為 ;
(2)補全條形統計圖:扇形統計圖中,![]() 類所對應的圓心角為 度;
類所對應的圓心角為 度;
(3)若該區共有七年級學生![]() 人,則愿意參加“學生課后延時服務”的人數大概是多少?
人,則愿意參加“學生課后延時服務”的人數大概是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
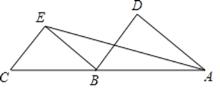
【題目】已知A,B,C三點在同一直線上,∠DAE=∠AEB,∠D=∠BEC,
(1)求證:BD∥CE;
(2)若∠C=70°,∠DAC=50°,求∠DBE的度數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com