
【題目】在平面直角坐標(biāo)系xOy中,拋物線y=x2﹣2mx+m2﹣1與y軸交于點(diǎn)C.
(1)試用含m的代數(shù)式表示拋物線的頂點(diǎn)坐標(biāo);
(2)將拋物線y=x2﹣2mx+m2﹣1沿直線y=﹣1翻折,得到的新拋物線與y軸交于點(diǎn)D,若m>0,CD=8,求m的值.
(3)已知A(﹣k+4,1),B(1,k﹣2),在(2)的條件下,當(dāng)線段AB與拋物線y=x2﹣2mx+m2﹣1只有一個(gè)公共點(diǎn)時(shí),請求出k的取值范圍.
【答案】(1)(m,﹣1);(2)m=2;(3)2﹣![]() ≤k<2+
≤k<2+![]() .
.
【解析】
(1)將拋物線的解析式化為頂點(diǎn)式即可求得結(jié)果;
(2)依題意根據(jù)對(duì)稱性求得OC=3,即可得m2﹣1=3,從而求得m的值;
(3)將點(diǎn)A(k+4,1),點(diǎn)B(1,k2)代入拋物線,此時(shí)是線段AB與拋物線剛相交的時(shí)候,結(jié)合圖象分析即可得k的取值范圍,再求出AB的解析式,根據(jù)直線與拋物線只有一個(gè)交點(diǎn)可求出k的另外一個(gè)取值.
解:(1)∵y=x22mx+m21=(xm)21,
∴拋物線的頂點(diǎn)坐標(biāo)為(m,1);
(2)由y=x22mx+m21得![]() ,
,
∵CD=8,依題意由對(duì)稱性可知,點(diǎn)C到直線y=1的距離為4,
∴OC=3,
∴m2﹣1=3,解得:m=±2,
∵m>0,
∴m=2;
(3)∵m=2,
∴拋物線為y=x24x+3,
當(dāng)拋物線經(jīng)過點(diǎn)A(k+4,1)時(shí),![]() 或
或![]() ;
;
當(dāng)拋物線經(jīng)過點(diǎn)B(1,k2)時(shí),k=2;
∴線段AB與拋物線y=x22mx+m21只有一個(gè)公共點(diǎn)時(shí),由圖象得:
![]() 或
或![]() ,
,
設(shè)直線AB的解析式為:y=ax+b,將點(diǎn)A(k+4,1),點(diǎn)B(1,k2)代入得:
![]() ,解得
,解得![]() ,
,
∴y=x+k3,
若直線AB與拋物線y=x22mx+m21只有一個(gè)公共點(diǎn),
則x24x+3=x+ k3,即x25x+6k=0,=0,
∴=254×(6k)=0,
解得:![]() ,此時(shí)線段AB與拋物線y=x24x+3只有一個(gè)公共點(diǎn),
,此時(shí)線段AB與拋物線y=x24x+3只有一個(gè)公共點(diǎn),
綜上所述:當(dāng)線段AB與拋物線y=x22mx+m21只有一個(gè)公共點(diǎn)時(shí),
k的取值范圍是:![]() 或
或![]() 或
或![]() .
.


 名校課堂系列答案
名校課堂系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
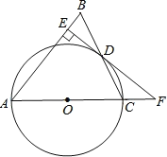
【題目】如圖,在△ABC中,AB=AC,以AC邊為直徑作![]() O交BC邊于點(diǎn)D,過點(diǎn)D作DE⊥AB于點(diǎn)E,ED、AC的延長線交于點(diǎn)F.
O交BC邊于點(diǎn)D,過點(diǎn)D作DE⊥AB于點(diǎn)E,ED、AC的延長線交于點(diǎn)F.
(1)求證:EF是![]() O的切線;
O的切線;
(2)若EB=6,且sin∠CFD=![]() ,求
,求![]() O的半徑.
O的半徑.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,拋物線![]() 與x軸交于點(diǎn)
與x軸交于點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() ,與y軸交于點(diǎn)C,且過點(diǎn)
,與y軸交于點(diǎn)C,且過點(diǎn)![]() .點(diǎn)P、Q是拋物線
.點(diǎn)P、Q是拋物線![]() 上的動(dòng)點(diǎn).
上的動(dòng)點(diǎn).
(1)求拋物線的解析式;
(2)當(dāng)點(diǎn)P在直線OD下方時(shí),求![]() 面積的最大值.
面積的最大值.
(3)直線OQ與線段BC相交于點(diǎn)E,當(dāng)![]() 與
與![]() 相似時(shí),求點(diǎn)Q的坐標(biāo).
相似時(shí),求點(diǎn)Q的坐標(biāo).

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某商品原價(jià)為100元,第一次漲價(jià)![]() ,第二次在第一次的基礎(chǔ)上又漲價(jià)
,第二次在第一次的基礎(chǔ)上又漲價(jià)![]() ,設(shè)平均每次增長的百分?jǐn)?shù)為x,那么x應(yīng)滿足的方程是
,設(shè)平均每次增長的百分?jǐn)?shù)為x,那么x應(yīng)滿足的方程是![]()
![]()
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某水果公司新購進(jìn)10000千克柑橘,每千克柑橘的成本為9元. 柑橘在運(yùn)輸、存儲(chǔ)過程中會(huì)有損壞,銷售人員從所有的柑橘中隨機(jī)抽取若干柑橘,進(jìn)行“柑橘損壞率”統(tǒng)計(jì),并把獲得的數(shù)據(jù)記錄如下:
柑橘總重量n/千克 | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 |
損壞柑橘重量m/千克 | 5.50 | 10.50 | 15.15 | 19.42 | 24.25 | 30.93 | 35.32 | 39.24 | 44.57 | 51.54 |
柑橘損壞的頻率 | 0.110 | 0.105 | 0.101 | 0.097 | 0.097 | 0.103 | 0.101 | 0.098 | 0.099 | 0.103 |
根據(jù)以上數(shù)據(jù),估計(jì)柑橘損壞的概率為 (結(jié)果保留小數(shù)點(diǎn)后一位);由此可知,去掉損壞的柑橘后,水果公司為了不虧本,完好柑橘每千克的售價(jià)至少為________元.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
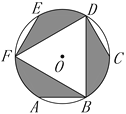
【題目】如圖所示是一個(gè)圓形飛鏢靶的示意圖,其中A,B,C,D,E,F是⊙O的六等分點(diǎn),如果向該飛鏢靶上任意投一枚飛鏢,則飛鏢落在陰影區(qū)域的概率是_______.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】綜合與探究:如圖,二次函數(shù)![]() 經(jīng)過點(diǎn)B(4,0)和點(diǎn)E(-2,-3)兩點(diǎn),與x軸的另一個(gè)交點(diǎn)為A.點(diǎn)D是線段BE上的動(dòng)點(diǎn),過點(diǎn)D作DF⊥BE,交y軸于點(diǎn)F,交拋物線于點(diǎn)P.
經(jīng)過點(diǎn)B(4,0)和點(diǎn)E(-2,-3)兩點(diǎn),與x軸的另一個(gè)交點(diǎn)為A.點(diǎn)D是線段BE上的動(dòng)點(diǎn),過點(diǎn)D作DF⊥BE,交y軸于點(diǎn)F,交拋物線于點(diǎn)P.
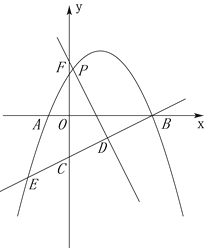
(1)求出拋物線和直線BE的解析式;
(2)當(dāng)△DCF≌△BOC時(shí),求出此時(shí)點(diǎn)D的坐標(biāo);
(3)設(shè)點(diǎn)P的橫坐標(biāo)為m.
①請寫出線段PD的長度為(用含m的式子表示);
②當(dāng)m為何值時(shí),線段PD有最大值,并寫出其最大值為多少?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】小明投資銷售一種進(jìn)價(jià)為每件20元的護(hù)眼臺(tái)燈.銷售過程中發(fā)現(xiàn),每月銷售量y(件)與銷售單價(jià)x(元)之間的關(guān)系可近似的看作一次函數(shù):y=﹣10x+500,在銷售過程中銷售單價(jià)不低于成本價(jià),而每件的利潤不高于成本價(jià)的60%.
(1)設(shè)小明每月獲得利潤為w(元),求每月獲得利潤w(元)與銷售單價(jià)x(元)之間的函數(shù)關(guān)系式,并確定自變量x的取值范圍.
(2)當(dāng)銷售單價(jià)定為多少元時(shí),每月可獲得最大利潤?每月的最大利潤是多少?
(3)如果小明想要每月獲得的利潤不低于2000元,那么小明每月的成本最少需要多少元?(成本=進(jìn)價(jià)×銷售量)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】據(jù)新浪網(wǎng)調(diào)查,在第十二屆全國人大二中全會(huì)后,全國網(wǎng)民對(duì)政府工作報(bào)告關(guān)注度非常高,大家關(guān)注的網(wǎng)民們關(guān)注的熱點(diǎn)話題分別有:消費(fèi)、教育、環(huán)保、反腐、及其它共五類,且關(guān)注五類熱點(diǎn)問題的網(wǎng)民的人數(shù)所占百分比如圖l所示,關(guān)注該五類熱點(diǎn)問題網(wǎng)民的人數(shù)的不完整條形統(tǒng)計(jì)如圖2所示,請根據(jù)圖中信息解答下列問題.
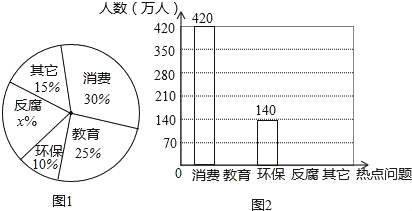
(1)求出圖l中關(guān)注“反腐”類問題的網(wǎng)民所占百分比x的值,并將圖2中的不完整的條形統(tǒng)計(jì)圖補(bǔ)充完整;
(2)為了深入探討政府工作報(bào)告,新浪網(wǎng)邀請成都市5名網(wǎng)民代表甲、乙、丙、丁、戊做客新浪訪談,且一次訪談只選2名代表,請你用列表法或畫樹狀圖的方法,求出一次所選代表恰好是甲和乙的概率.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com