某公司有甲種原料260kg，乙種原料270kg，計劃用這兩種原料生產A、B兩種產品共40件．生產每件A種產品需甲種原料8kg，乙種原料5kg，可獲利潤900元；生產每件B種產品需甲種原料4kg，乙種原料9kg，可獲利潤1100元．設安排生產A種產品x件．
（1）完成下表
| | 甲（kg） | 乙（kg） | 件數（件） |
| A | | 5x | x |
| B | 4（40-x） | | 40-x |
小學教材全測系列答案
小學數學口算題卡脫口而出系列答案科目：初中數學 來源： 題型：解答題
已知：甲、乙兩車分別從相距300千米的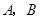
兩地同時出發相向而行，其中甲到
地后立即返回，下圖是它們離各自出發地的距離
（千米）與行駛時間
（小時）之間的函數圖象．
（1）求甲車離出發地的距離（千米）與行駛時間（小時）之間的函數關系式，并寫出自變量的取值范圍；
（2）當它們行駛到與各自出發地的距離相等時，用了
小時，求乙車離出發地的距離（千米）與行駛時間（小時）之間的函數關系式；
（3）在（2）的條件下，求它們在行駛的過程中相遇的時間．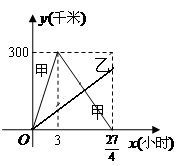
查看答案和解析>>
科目：初中數學 來源： 題型：解答題
如圖，一次函數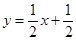
的圖象與x軸交于點A，與y軸交于點B，與反比例函數
的圖象在第一象限內交于點C，CD⊥x軸于點D，OD＝2AO，求反比例函數
的表達式． 
查看答案和解析>>
科目：初中數學 來源： 題型：解答題
如圖，二次函數y=(x-2)2+m的圖象與y軸交于點C，點B是點C關于該二次函數圖象的對稱軸對稱的點，已知一次函數y=kx+b的圖象上的點A（1,0）及B.
（1）求二次函數與一次函數的解析式；
（2）根據圖象，寫出滿足kx+b
（x-2）2+m的x的取值范圍.
查看答案和解析>>
科目：初中數學 來源： 題型：解答題
一農民帶了若干千克自產的土豆進城出售，為了方便，他帶了一些零錢備用，按市場價售出一些后，又降價出售， 售出土豆千克數與他手中持有的錢(含備用零錢)的關系如圖所示，結合圖象回答下列問題：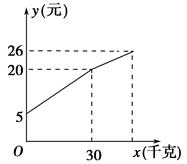
(1) 農民自帶的零錢是多少？
(2) 降價前他每千克土豆出售的價格是多少？
(3) 降價后他按每千克0.4元將剩余土豆售完，這時他手中的錢(含備用零錢) 是26元，問他一共帶了多少千克土豆．
查看答案和解析>>
科目：初中數學 來源： 題型：解答題
如圖，一次函數y1＝kx＋b的圖象與反比例函數y2＝
的圖象相交于點A(2，3)和點B，與x軸相交于點C(8，0)．
(1)求這兩個函數的解析式；
(2)當x取何值時，y1＞y2.
查看答案和解析>>
科目：初中數學 來源： 題型：解答題
如圖，在平面直角坐標系中，O為坐標原點，點A的坐標為（0，4），點B的坐標為（4，0），點C的坐標為（-4，0），點P在射線AB上運動，連結CP與y軸交于點D，連結BD．過P，D，B三點作⊙Q與y軸的另一個交點為E，延長DQ交⊙Q于點F，連結EF，BF．
（1）求直線AB的函數解析式；
（2）當點P在線段AB（不包括A，B兩點）上時．
①求證：∠BDE=∠ADP；
②設DE=x，DF=y．請求出y關于x的函數解析式；
（3）請你探究：點P在運動過程中，是否存在以B，D，F為頂點的直角三角形，滿足兩條直角邊之比為2：1？如果存在，求出此時點P的坐標：如果不存在，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：解答題
如圖，一次函數y1=x+1的圖象與反比例函數
（k為常數，且
）的圖象都經過點A(m,2).
（1）求點A的坐標及反比例函數的解析式；
（2）觀察圖象，當x>0時，直接寫出y1與y2的大小關系.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
是一張放在平面直角坐標系中的矩形紙片,
為原點,點
在
軸的正半軸上,
,在
上取一點
,將紙片沿
翻折,使點
邊上的點
處,求直線
的解析式.