
【題目】問題提出;怎樣計算1×2+2×3+3×4+…+(n﹣1)×n呢?
材料學習
計算1+2+3…+n
因為1= ![]() (1×2﹣0×1);2=
(1×2﹣0×1);2= ![]() (2×3﹣1×2);3=
(2×3﹣1×2);3= ![]() (3×4﹣2×3)
(3×4﹣2×3)
…,n= ![]() [n(n+1)﹣(n﹣1)n]
[n(n+1)﹣(n﹣1)n]
所以1+2+3+…+n
= ![]() (1×2﹣0×1)+
(1×2﹣0×1)+ ![]() (2×3﹣1×2)+
(2×3﹣1×2)+ ![]() (3×4﹣2×3)+…+
(3×4﹣2×3)+…+ ![]() [n(n+1)﹣(n﹣1)n]
[n(n+1)﹣(n﹣1)n]
= ![]() [1×2﹣0×1+2×3﹣1×2+3×4﹣2×3+…+n(n+1)﹣(n﹣1)n]=
[1×2﹣0×1+2×3﹣1×2+3×4﹣2×3+…+n(n+1)﹣(n﹣1)n]= ![]() n(n+1)
n(n+1)
(1)探究應用
觀察規律:①1×2= ![]() (1×2×3﹣0×12);②2×3=
(1×2×3﹣0×12);②2×3= ![]() (2×3×4﹣1×2×3);
(2×3×4﹣1×2×3);
③3×4= ![]() (3×4×5﹣2×3×4);…
(3×4×5﹣2×3×4);…
猜想歸納:
根據(1)中觀察的規律直接寫出:4×5= ![]() ()
()
(n﹣1)×n= ![]() []
[]
問題解決:
1×2+2×3+3×4+4×5…+(n﹣1)×n
= ![]() (1×2×3﹣0×1×2)+
(1×2×3﹣0×1×2)+ ![]() (2×3×4﹣1×2×3)+
(2×3×4﹣1×2×3)+ ![]() (3×4×5﹣2×3×4)+…+
(3×4×5﹣2×3×4)+…+ ![]() []
[]
=
(2)拓展延伸
根據上面的規律,請直接寫出1×2×3+2×3×4+3×4×5+…+(n﹣2)(n﹣1)n= .
【答案】
(1)4×5×6﹣3×4×5;(n﹣1)n(n+1)﹣(n﹣2)(n﹣1)n;(n﹣1)n(n+1)﹣(n﹣2)(n﹣1)n;![]() [1×2×3﹣0×1×2+2×3×4﹣1×2×3+3×4×5﹣2×3×4+…+(n﹣1)n(n+1)﹣(n﹣2)(n﹣1)n]=
[1×2×3﹣0×1×2+2×3×4﹣1×2×3+3×4×5﹣2×3×4+…+(n﹣1)n(n+1)﹣(n﹣2)(n﹣1)n]= ![]() (n﹣1)n(n+1)
(n﹣1)n(n+1)![]()
(2)![]()
(n﹣2)(n﹣1)n(n+1)
【解析】解:(1)4×5= ![]() (4×5×6﹣3×4×5);
(4×5×6﹣3×4×5);
1×2+2×3+3×4+4×5…+(n﹣1)×n
= ![]() (1×2×3﹣0×1×2)+
(1×2×3﹣0×1×2)+ ![]() (2×3×4﹣1×2×3)+
(2×3×4﹣1×2×3)+ ![]() (3×4×5﹣2×3×4)+…+
(3×4×5﹣2×3×4)+…+ ![]() [(n﹣1)n(n+1)﹣(n﹣2)(n﹣1)n]
[(n﹣1)n(n+1)﹣(n﹣2)(n﹣1)n]
= ![]() [1×2×3﹣0×1×2+2×3×4﹣1×2×3+3×4×5﹣2×3×4+…+(n﹣1)n(n+1)﹣(n﹣2)(n﹣1)n]
[1×2×3﹣0×1×2+2×3×4﹣1×2×3+3×4×5﹣2×3×4+…+(n﹣1)n(n+1)﹣(n﹣2)(n﹣1)n]
= ![]() (n﹣1)n(n+1);
(n﹣1)n(n+1);
2)問題解決:1×2×3+2×3×4+3×4×5+…+(n﹣2)(n﹣1)n
= ![]() (1×2×3×4﹣0×1×2×3)+
(1×2×3×4﹣0×1×2×3)+ ![]() (2×3×4×5﹣1×2×3×4)+
(2×3×4×5﹣1×2×3×4)+ ![]() (3×4×5×6﹣2×3×4×5)+…+
(3×4×5×6﹣2×3×4×5)+…+ ![]() [(n﹣2)(n﹣1)n(n+1)﹣(n﹣3)(n﹣2)(n﹣1)n]
[(n﹣2)(n﹣1)n(n+1)﹣(n﹣3)(n﹣2)(n﹣1)n]
= ![]() [1×2×3×4﹣0×1×2×3+2×3×4×5﹣1×2×3×4+3×4×5×6﹣2×3×4×5+…+(n﹣2)(n﹣1)n(n+1)﹣(n﹣3)(n﹣2)(n﹣1)n]
[1×2×3×4﹣0×1×2×3+2×3×4×5﹣1×2×3×4+3×4×5×6﹣2×3×4×5+…+(n﹣2)(n﹣1)n(n+1)﹣(n﹣3)(n﹣2)(n﹣1)n]
= ![]() (n﹣2)(n﹣1)n(n+1).
(n﹣2)(n﹣1)n(n+1).
所以答案是:4×5×6﹣3×4×5,(n﹣1)n(n+1)﹣(n﹣2)(n﹣1)n;(n﹣1)n(n+1)﹣(n﹣2)(n﹣1)n,= ![]() [1×2×3﹣0×1×2+2×3×4﹣1×2×3+3×4×5﹣2×3×4+…+(n﹣1)n(n+1)﹣(n﹣2)(n﹣1)n],
[1×2×3﹣0×1×2+2×3×4﹣1×2×3+3×4×5﹣2×3×4+…+(n﹣1)n(n+1)﹣(n﹣2)(n﹣1)n], ![]() (n﹣1)n(n+1);
(n﹣1)n(n+1); ![]() (n﹣2)(n﹣1)n(n+1).
(n﹣2)(n﹣1)n(n+1).
【考點精析】掌握有理數的四則混合運算是解答本題的根本,需要知道在沒有括號的不同級運算中,先算乘方再算乘除,最后算加減.


 金牌教輔培優優選卷期末沖刺100分系列答案
金牌教輔培優優選卷期末沖刺100分系列答案科目:初中數學 來源: 題型:
【題目】(本題滿分10分)如圖,已知AB是⊙O的直徑,點C在⊙O上,過點C的直線與AB的延長線交于點P,AC=PC,∠COB=2∠PCB.
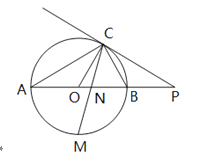
(1)求證:PC是⊙O的切線;
(2)求證:BC=![]() AB;
AB;
(3)點M是弧AB的中點,CM交AB于點N,若AB=4,求MN·MC的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個四邊形的三個內角的度數依次如下,那么其中是平行四邊形的是( )
A. 88°,108°,88° B. 88°,104°,88°
C. 88°,92°,92° D. 88°,92°,88°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某種速凍水餃的儲藏溫度是﹣18±2℃,四個冷藏室的溫度如下,則不適合儲藏此種水餃的是( )
A. ﹣17℃ B. ﹣18℃ C. ﹣19℃ D. ﹣22℃
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AOB是一條直線,∠AOC=60°,OD,OE分別是∠AOC和∠BOC的平分線,則圖中互補的角有( ) 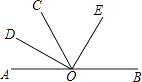
A.5對
B.6對
C.7對
D.8對
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com