
【題目】如圖,![]() 中,
中,![]() ,
,![]() ,以
,以![]() 為圓心,
為圓心,![]() 長為半徑畫弧,分別交
長為半徑畫弧,分別交![]() 、
、![]() 于
于![]() 、
、![]() 兩點,連接
兩點,連接![]() 、
、![]() ,則除
,則除![]() 外,圖中是等腰三角形的還有( )
外,圖中是等腰三角形的還有( )
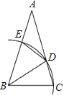
A.1個B.2個C.3個D.4個
【答案】D
【解析】
等腰三角形還有△BDC,△BED,△BAD,△AED,根據半徑相等得出△BDC和△BED是等腰三角形,根據等腰三角形性質和三角形的內角和定理即可推出其它三角形也是等腰三角形.
解:除△ABC外,等腰三角形還有△BDC,△BED,△BAD,△AED,
理由是:∵BD=BC=BE,
∴△BDC和△BED是等腰三角形,
∵∠A=36°,AC=AB,
∴∠C=∠ABC=![]() (180°∠A)=72°,
(180°∠A)=72°,
∵BD=BC,
∴∠BDC=∠C=72°,
∴∠CBD=180°72°72°=36°,
∴∠ABD=72°36°=36°=∠A,
∴BD=AD,即△ABD是等腰三角形,
∵∠ABD=36°,BE=BD,
∴∠BDE=∠BED=![]() (180°∠ABD)=72°,
(180°∠ABD)=72°,
∵∠ADE=180°72°72°=36°=∠A,
∴AE=DE,
∴△AED是等腰三角形,
故選:D.


 云南師大附小一線名師提優作業系列答案
云南師大附小一線名師提優作業系列答案 沖刺100分單元優化練考卷系列答案
沖刺100分單元優化練考卷系列答案科目:初中數學 來源: 題型:
【題目】如圖,矩形OABC的邊OC在y軸上,邊OA在x軸上,C點坐標為(0,3),點D是線段OA的一個動點,連接CD,以CD為邊作矩形CDEF,使邊EF過點B,已知所作矩形CDEF的面積為12,連接OF,則在點D的運動過程中,線段OF的最大值為__.
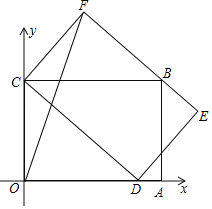
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為宣傳節約用水,小強隨機調查了某小區部分家庭3月份的用水情況,并將收集的數據整理成如下統計圖.
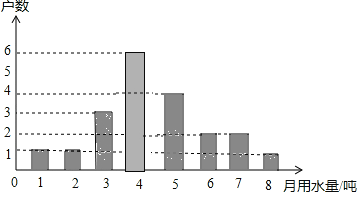
(1)小明一共調查了多少戶家庭?
(2)求所調查家庭3月份用水量的眾數、中位數和平均數;
(3)若該小區有800戶居民,請你估計這個小區3月份的總用水量是多少噸?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】圖①是一個三角形,分別連接這個三角形三邊的中點得到圖②,再分別連接圖②中間的小三角形三邊的中點,得到圖③.

(1)圖②有__________個三角形;圖③有________個三角形;
(2)按上面的方法繼續下去,第10個圖有_________個三角形,第![]() 個圖形中有_______個三角形.(用含
個圖形中有_______個三角形.(用含![]() 的代數式表示)
的代數式表示)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在黃岡長江大橋的東端一處空地上,有一塊矩形的標語牌ABCD(如圖4所示).已知標語牌的高AB=5 m,在地面的點E處,測得標語牌點A的仰角為30°,在地面的點F處,測得標語牌點A的仰角為75°,且點E,F,B,C在同一直線上.求點E與點F之間的距離(計算結果精確到0.1 m,參考數據:![]() ≈1.41,
≈1.41,![]() ≈1.73).
≈1.73).
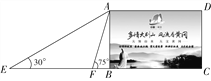
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有一個數值轉換器,原理如圖所示,若開始輸入x的值是5,可發現第1次輸出的結果是16,第2次輸出的結果是8,(第3次輸出的結果是4,依次繼續下去,第101次輸出的結果是( )

A.1B.2C.4D.8
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為增強公民的節約意識,合理利用天然氣資源,某市自![]() 月
月![]() 日起對市區民用管道天然氣價格進行調整,實行階梯式氣價,調整后的收費價格如表所示:
日起對市區民用管道天然氣價格進行調整,實行階梯式氣價,調整后的收費價格如表所示:
每月用氣量 | 單價(元 |
不超出 |
|
超出 |
|
超出 |
|
(1)若某用戶![]() 月份用氣量為
月份用氣量為![]() ,交費多少元?
,交費多少元?
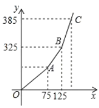
(2)調價后每月支付燃氣費用![]() (單位:元)與每月用氣量
(單位:元)與每月用氣量![]() (單位:
(單位:![]() )的關系如圖所示,求
)的關系如圖所示,求![]() 與
與![]() 的解析式及
的解析式及![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
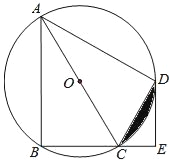
【題目】如圖,四邊形ABCD是⊙O的內接四邊形,![]() ,AC為直徑,DE⊥BC,垂足為E.
,AC為直徑,DE⊥BC,垂足為E.
(1)求證:CD平分∠ACE;
(2)若AC=9,CE=3,求CD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知∠A=∠D=90°,E、F在線段BC上,DE與AF交于點O,且AB=CD,BE=CF.
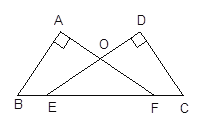
求證:(1)Rt△ABF≌Rt△DCE;(2)OE=OF .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com