
【題目】如圖,△ABC是等邊三角形,點D在AC上,點E在BC的延長線上,且BD=DE.
(1)若點D是AC的中點,如圖1,求證:AD=CE
(2)若點D不是AC的中點,如圖2,試判斷AD與CE的數量關系,并證明你的結論:(提示:過點D作DF∥BC,交AB于點F)

【答案】(1)證明見解析;(2)AD=CE,證明見解析.
【解析】分析:(1)求出∠E=∠CDE,推出CD=CE,根據等腰三角形性質求出AD=DC,即可得出答案;(2)過D作DF∥BC,交AB于F,證△BFD≌△DCE,推出DF=CE,證△ADF是等邊三角形,推出AD=DF,即可得出答案.
本題解析:
(1)證明:∵△ABC是等邊三角形,∴∠ABC=∠ACB=60°,AB=AC=BC,∵D為AC中點,∴∠DBC=30°,AD=DC,∵BD=DE,∴∠E=∠DBC=30°∵∠ACB=∠E+∠CDE,
∴∠CDE=30°=∠E,∴CD=CE,∵AD=DC,∴AD=CE;
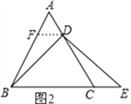
(2)AD=CE,如圖2,過D作DF∥BC,交AB于F,
則∠ADF=∠ACB=60°,∵∠A=60°,∴△AFD是等邊三角形,
∴AD=DF=AF,∠AFD=60°,∴∠BFD=∠DCE=180°﹣60°=120°,
∵DF∥BC,∴∠FDB=∠DBE=∠E,
在△BFD和△DCE中 ,∴△BFD≌△DCE,∴CE=DF=AD,即AD=CE.
,∴△BFD≌△DCE,∴CE=DF=AD,即AD=CE.


科目:初中數學 來源: 題型:
【題目】甲、乙兩人兩次同時在同一家糧店購買糧食(假設兩次購買糧食的單價不相同),甲每次購買
糧食100千克,乙每次購買糧食用去100元.
(1)假設![]() 、
、![]() 分別表示兩次購買糧食時的單價(單位:元/千克),試用含
分別表示兩次購買糧食時的單價(單位:元/千克),試用含![]() 、
、![]() 的代數式表示:甲兩次購
的代數式表示:甲兩次購
買糧食共需付款 元,乙兩次共購買 千克糧食;若甲兩次購買糧食的平均單價為每千
克![]() 元,乙兩次購買糧食的平均單價為每千克
元,乙兩次購買糧食的平均單價為每千克![]() 元,則
元,則![]() = ,
= ,![]() = .
= .
(2)若誰兩次購買糧食的平均單價低,誰購買糧食的方式就較合算.請你判斷甲、乙兩人購買糧食的方式哪一個較合算,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖![]() ,平行四邊形
,平行四邊形![]() 中,對角線
中,對角線![]() 、
、![]() 交于點
交于點![]() .將直線
.將直線![]() 繞點
繞點![]() 順時針旋轉分別交
順時針旋轉分別交![]() 、
、![]() 于點
于點![]() 、
、![]() .
.
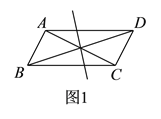
(![]() )在旋轉過程中,線段
)在旋轉過程中,線段![]() 與
與![]() 的數量關系是__________.
的數量關系是__________.
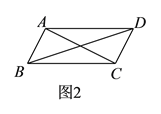
(![]() )如圖
)如圖![]() ,若
,若![]() ,當旋轉角至少為__________
,當旋轉角至少為__________![]() 時,四邊形
時,四邊形![]() 是平行四邊形,并證明此時的四邊形是
是平行四邊形,并證明此時的四邊形是![]() 是平行四邊形.
是平行四邊形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某服裝廠計劃生產A,B兩款校服共500件,這兩款校服的成本、售價如表所示:
類別 | 成本(元/件) | 售價(元/件) |
A款 | 30 | 45 |
B款 | 50 | 70 |
(1)求校服廠家銷售完這批校服時所獲得的利潤y(元)與A款校服的生產數量x(件)之間的函數關系.
(2)若廠家計劃B款校服的生產數量不超過A款校服的生產數量的4倍,應怎樣安排生產才能使校服廠家在銷售完這批校服時獲得利潤最多?此時獲得利潤為多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義新運算:對于任意實數a,b,都有a![]() b=a(a-b)+1,等式右邊是通常的加法、減法及乘法運算,比如:2
b=a(a-b)+1,等式右邊是通常的加法、減法及乘法運算,比如:2![]() 5=2×(2-5)+1=2×(-3)+1=-6+1=-5.
5=2×(2-5)+1=2×(-3)+1=-6+1=-5.
(1)求(-2) ![]() 3的值;
3的值;
(2)若3![]() x的值小于13,求x的取值范圍,并在如圖所示的數軸上表示出來.
x的值小于13,求x的取值范圍,并在如圖所示的數軸上表示出來.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,每個小正方形的邊長為1個單位,每個小方格的頂點叫格點.
⑴畫出△ABC向右平移4個單位后得到的△A1B1C1;
⑵圖中AC與A1C1的關系是: ;
⑶畫出△ABC中AB邊上的中線CD;
⑷△ACD的面積為 .

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀與思考:整式乘法與因式分解是方向相反的變形
由(x+p)(x+q)=x2+(p+q)x+pq得x2+(p+q)x+pq=(x+p)(x+q)
利用這個式子可以將某些二次項系數是1的二次三項式分解因式,
例如:將式子x2+3x+2分解因式.
分析:這個式子的常數項2=1×2一次項系數3=1+2
所以x2+3x+2=x2+(1+2)x=1×2
解:x2+3x+2=(x+)(x+2)
請仿照上面的方法,解答下列問題:
(1)分解因式:x2+6x-27=__________________;
(2)若x2+px+8可分解為兩個一次因式的積,則整數![]() 的所有可能值是_________________;
的所有可能值是_________________;
(3)利用因式分解法解方程:x2-4x-12=0..
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com