
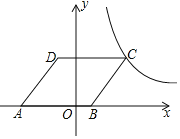
【題目】如圖,在平面直角坐標系中,點O為坐標原點,菱形ABCD的頂點B在x軸的正半軸上,點A坐標為(-4,0),點D的坐標為(-1,4),反比例函數![]() 的圖象恰好經過點C,則k的值為______.
的圖象恰好經過點C,則k的值為______.
 金鑰匙試卷系列答案
金鑰匙試卷系列答案科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD是平行四邊形,![]() //
//![]() ,且分別交對角線AC于點E,F,連接BE,DF.
,且分別交對角線AC于點E,F,連接BE,DF.
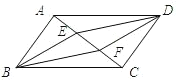
(1)求證:AE=CF;
(2)若BE=DE,求證:四邊形EBFD為菱形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,AB為
中,AB為![]() 的直徑,C為
的直徑,C為![]() 上一點,P是
上一點,P是![]() 的中點,過點P作AC的垂線,交AC的延長線于點D.
的中點,過點P作AC的垂線,交AC的延長線于點D.
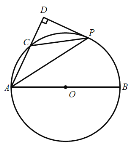
(1)求證:DP是![]() 的切線;
的切線;
(2)若AC=5,![]() ,求AP的長.
,求AP的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:△ABC和△ADE按如圖所示方式放置,點D在△ABC內,連接BD、CD和CE,且∠DCE=90°.

(1)如圖①,當△ABC和△ADE均為等邊三角形時,試確定AD、BD、CD三條線段的關系,并說明理由;
(2)如圖②,當BA=BC=2AC,DA=DE=2AE時,試確定AD、BD、CD三條線段的關系,并說明理由;
(3)如圖③,當AB:BC:AC=AD:DE:AE=m:n:p時,請直接寫出AD、BD、CD三條線段的關系.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知一個矩形紙片![]() ,將該紙片放置在平面直角坐標系中,點
,將該紙片放置在平面直角坐標系中,點![]() ,點
,點![]() ,點P為
,點P為![]() 邊上的動點.
邊上的動點.
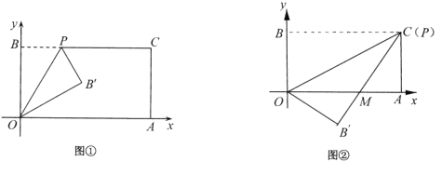
(1)如圖①,經過點O、P折疊該紙片,得點![]() 和折痕
和折痕![]() .當點P的坐標為
.當點P的坐標為![]() 時,求
時,求![]() 的度數;
的度數;
(2)如圖②,當點P與點C重合時,經過點O、P折疊紙片,使點B落在點![]() 的位置,
的位置,![]() 與
與![]() 交于點M,求點M的坐標;
交于點M,求點M的坐標;
(3)過點P作直線![]() ,交
,交![]() 于點Q,再取
于點Q,再取![]() 中點T,
中點T,![]() 中點N,分別以
中點N,分別以![]() ,
,![]() ,
,![]() ,
,![]() 為折痕,依次折疊該紙片,折疊后點O的對應點與點B的對應點恰好重合,且落在線段
為折痕,依次折疊該紙片,折疊后點O的對應點與點B的對應點恰好重合,且落在線段![]() 上,A、C的對應點也恰好重合,也落在線段
上,A、C的對應點也恰好重合,也落在線段![]() 上,求此時點P的坐標(直接寫出結果即可).
上,求此時點P的坐標(直接寫出結果即可).
查看答案和解析>>
科目:初中數學 來源: 題型:
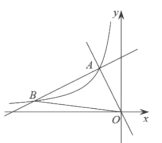
【題目】如圖,在平面直角坐標系![]() 中,一次函數
中,一次函數![]() 和
和![]() 的圖象相交于點
的圖象相交于點![]() ,反比例函數
,反比例函數![]() 的圖象經過點
的圖象經過點![]() .
.
(1)求反比例函數的表達式;
(2)設一次函數![]() 的圖象與反比例函數
的圖象與反比例函數![]() 的圖象的另一個交點為
的圖象的另一個交點為![]() ,連接
,連接![]() ,求
,求![]() 的面積.
的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
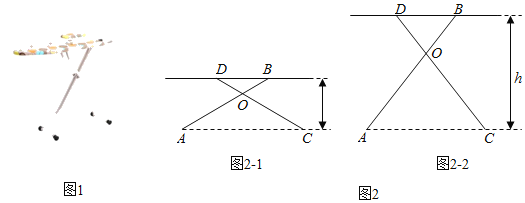
【題目】有一種升降熨燙臺如圖1所示,其原理是通過改變兩根支撐桿夾角的度數來調整熨燙臺的高度.圖2是這種升降熨燙臺的平面示意圖.AB和CD是兩根相同長度的活動支撐桿,點O是它們的連接點,OA=OC,h(cm)表示熨燙臺的高度.
(1)如圖2﹣1.若AB=CD=110cm,∠AOC=120°,求h的值;
(2)愛動腦筋的小明發現,當家里這種升降熨燙臺的高度為120cm時,兩根支撐桿的夾角∠AOC是74°(如圖2﹣2).求該熨燙臺支撐桿AB的長度(結果精確到lcm).
(參考數據:sin37°≈0.6,cos37°≈0.8,sin53°≈0.8,cos53°≈0.6.)
查看答案和解析>>
科目:初中數學 來源: 題型:
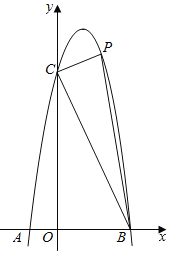
【題目】如圖,已知拋物線y=ax2+bx+6經過兩點A(﹣1,0),B(3,0),C是拋物線與y軸的交點.
(1)求拋物線的解析式;
(2)點P(m,n)在平面直角坐標系第一象限內的拋物線上運動,設△PBC的面積為S,求S關于m的函數表達式(指出自變量m的取值范圍)和S的最大值;
(3)點M在拋物線上運動,點N在y軸上運動,是否存在點M、點N使得∠CMN=90°,且△CMN與△OBC相似,如果存在,請求出點M和點N的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
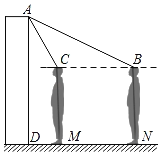
【題目】某校為檢測師生體溫,在校門安裝了某型號測溫門.如圖為該測溫門截面示意圖,已知測溫門AD的頂部A處距地面高為2.2m,為了解自己的有效測溫區間.身高1.6m的小聰做了如下實驗:當他在地面N處時測溫門開始顯示額頭溫度,此時在額頭B處測得A的仰角為18°;在地面M處時,測溫門停止顯示額頭溫度,此時在額頭C處測得A的仰角為60°.求小聰在地面的有效測溫區間MN的長度.(額頭到地面的距離以身高計,計算精確到0.1m,sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com