
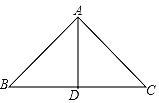
【題目】如圖,在△ABC中,AB=AC=2,BC=![]() ,且∠BAC=120°,點(diǎn)D是線段BC上的一動(dòng)點(diǎn)(不與點(diǎn)B、C重合),連接AD,作∠ADE=30°,DE交AC于點(diǎn)E.
,且∠BAC=120°,點(diǎn)D是線段BC上的一動(dòng)點(diǎn)(不與點(diǎn)B、C重合),連接AD,作∠ADE=30°,DE交AC于點(diǎn)E.
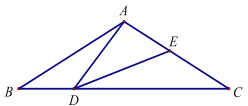
(1)求證:∠BAD∠EDC;
(2)當(dāng)BD= 時(shí),△ABD≌△EDC,并說(shuō)明理由.
(3)當(dāng)△ADE是直角三角形時(shí),求AD的長(zhǎng)?
【答案】(1)證明見(jiàn)解析;(2)答案見(jiàn)解析;(3)![]() 或1
或1
【解析】
(1)根據(jù)等腰三角形的性質(zhì)及三角形內(nèi)角和定理得出∠B=30°,然后根據(jù)三角形外角的性質(zhì)即可得出結(jié)論;
(2)先求出DC的長(zhǎng),可得到AB=DC.根據(jù)ASA即可證明△ABD≌△EDC;
(3)分兩種情況討論:①當(dāng)∠DAE=90°時(shí),△CAD是含30°角的直角三角形,可得出AC=![]() AD=2,求出AD的長(zhǎng)即可.
AD=2,求出AD的長(zhǎng)即可.
②當(dāng)∠DEA=90°時(shí),∠DAE=∠BAD=60°,得到△ABD是含30°角的直角三角形,即可得到AD的長(zhǎng).
(1)∵∠BAC=120°,AB=AC,∴∠B=∠C=30°.
又∵∠ADC=∠B+∠BAD,∴∠ADE+∠EDC=∠B+∠BAD.
又∵∠ADE=30°,∴∠BAD=∠EDC.
(2)當(dāng)BD=![]() 時(shí),△ABD≌△EDC.理由如下:
時(shí),△ABD≌△EDC.理由如下:
∵BD=![]() ,BC=
,BC=![]() ,∴DC=
,∴DC=![]() =2,∴AB=DC.
=2,∴AB=DC.
在△ABD和△EDC中,∵∠B=∠C,AB=DC,∠BAD=∠EDC,∴△ABD≌△EDC.
(3)①當(dāng)∠DAE=90°時(shí).
∵∠C=30°,∴AC=![]() AD=2,∴AD=
AD=2,∴AD=![]() =
=![]() .
.
②當(dāng)∠DEA=90°時(shí),∠DAE=∠BAD=60°.
又∵∠B=30°,∴∠ADB=90°,∴AD=![]() AB=1.
AB=1.
綜上所述:當(dāng)△ADE 是直角三角形時(shí),AD=![]() 或1.
或1.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖所示,正比例函數(shù) ![]() 的圖象與反比例函數(shù)
的圖象與反比例函數(shù) ![]()
![]() 在第一象限的圖象交于點(diǎn)
在第一象限的圖象交于點(diǎn) ![]() ,過(guò)點(diǎn)
,過(guò)點(diǎn) ![]() 作
作 ![]() 軸的垂線,垂足為
軸的垂線,垂足為 ![]() ,已知△OAM的面積為1.
,已知△OAM的面積為1.
(1)求反比例函數(shù)的解析式;
(2)如果點(diǎn) ![]() 為反比例函數(shù)在第一象限圖象上的點(diǎn)(點(diǎn)
為反比例函數(shù)在第一象限圖象上的點(diǎn)(點(diǎn) ![]() 與點(diǎn)
與點(diǎn) ![]() 不重合),且點(diǎn)
不重合),且點(diǎn) ![]() 的橫坐標(biāo)為1,在
的橫坐標(biāo)為1,在 ![]() 軸上求一點(diǎn)
軸上求一點(diǎn) ![]() ,使
,使 ![]() 最小.
最小.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】計(jì)算
(1)﹣![]() ﹣(+13)+(﹣
﹣(+13)+(﹣![]() )﹣(﹣17)
)﹣(﹣17)
(2)﹣22+3÷(﹣1)2017﹣|﹣4|×5
(3)先化簡(jiǎn)再求值﹣3(2x2﹣xy)+4(x2+xy﹣6),其中x=﹣1,y=2.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,反比例函數(shù)y= ![]() (k≠0)與一次函數(shù)y=kx+k(k≠0)在同一平面直角坐標(biāo)系內(nèi)的圖象可能是( )
(k≠0)與一次函數(shù)y=kx+k(k≠0)在同一平面直角坐標(biāo)系內(nèi)的圖象可能是( )
A.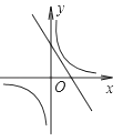
B.
C.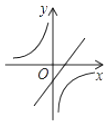
D.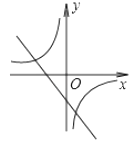
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】填空:
(1)(-5a4)·(-8ab2)=___.
(2)3x2y·![]() ·(5xy2)=___.
·(5xy2)=___.
(3)![]() (2x-3y)=___.
(2x-3y)=___.
(4)(-2ab)·(3a2-2ab-4b2)=___.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,∠BAC=90°,AD⊥BC,垂足為點(diǎn) D.下列說(shuō)法中:①∠B的余角只有∠BAD;②∠B=∠C;③線段 AB 的長(zhǎng)度表示點(diǎn) B 到直線 AC 的距離;④AB·AC=BC·AD;一定正確的有( )
A. 1 個(gè) B. 2 個(gè) C. 3 個(gè) D. 4 個(gè)
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】△ABC在平面直角坐標(biāo)系中的位置如圖所示.
(1)作出△ABC關(guān)于![]() 軸對(duì)稱(chēng)的△A1B1C1,并寫(xiě)出△A1B1C1各頂點(diǎn)的坐標(biāo);
軸對(duì)稱(chēng)的△A1B1C1,并寫(xiě)出△A1B1C1各頂點(diǎn)的坐標(biāo);
(2)將△ABC向右平移6個(gè)單位,作出平移后的△A2B2C2,并寫(xiě)出△A2B2C2各頂點(diǎn)的坐標(biāo);
(3)觀察△A1B1C和△A2B2C2,它們是否關(guān)于某直線對(duì)稱(chēng)?若是,請(qǐng)用實(shí)線條畫(huà)出對(duì)稱(chēng)軸。

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】計(jì)算
(1)3x3x9﹣2xx3x8
(2)﹣12+20160+(![]() )2017×(﹣4)2018
)2017×(﹣4)2018
(3)(x+4)(x﹣4)﹣(x﹣2)2
(4)ab(a+b)﹣(a﹣b)(a2+b2)
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】本學(xué)期學(xué)習(xí)了分式方程的解法,下面是晶晶同學(xué)的解題過(guò)程:
解方程 ![]()
解:整理,得: ![]() …………………………第①步
…………………………第①步
去分母,得: ![]() …………………………第②步
…………………………第②步
移項(xiàng),得: ![]() ……………………… 第③步
……………………… 第③步
合并同類(lèi)項(xiàng),得: ![]() ……………………… 第④步
……………………… 第④步
系數(shù)化1,得: ![]() …………………………第⑤步
…………………………第⑤步
檢驗(yàn):當(dāng)![]() 時(shí),
時(shí),![]()
所以原方程的解是![]() . ………………………第⑥步
. ………………………第⑥步
上述晶晶的解題過(guò)程從第_____步開(kāi)始出現(xiàn)錯(cuò)誤,錯(cuò)誤的原因是_________________.請(qǐng)你幫晶晶改正錯(cuò)誤,寫(xiě)出完整的解題過(guò)程.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com