
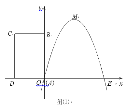
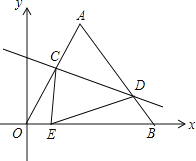
【題目】如圖(1),已知拋物線經(jīng)過坐標(biāo)原點(diǎn)O和x軸上另一點(diǎn)E,頂點(diǎn)M的坐標(biāo)為(2,4);矩形ABCD的頂點(diǎn)A與點(diǎn)O重合,AD、AB分別在x軸、y軸上,且AD=2,AB=3.
(1)求直線y=3與拋物線交點(diǎn)的坐標(biāo);
(2)將矩形ABCD以每秒1個(gè)單位長(zhǎng)度的速度從圖⑴所示的位置沿x軸的正方向勻速平行移動(dòng),同時(shí)一動(dòng)點(diǎn)P也以相同的速度從點(diǎn)A出發(fā)向B勻速移動(dòng),設(shè)它們運(yùn)動(dòng)的時(shí)間為t秒(0≤t≤3),直線AB與該拋物線的交點(diǎn)為N(如圖(2)所示).
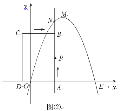
①當(dāng)![]() 時(shí),判斷點(diǎn)P是否在直線ME上,并說明理由;
時(shí),判斷點(diǎn)P是否在直線ME上,并說明理由;
②設(shè)以P、N、C、D為頂點(diǎn)的多邊形面積為S,試問S是否存在最大值?若存在,求出這個(gè)最大值;若不存在,請(qǐng)說明理由.
【答案】(1)直線![]() 與拋物線交點(diǎn)的坐標(biāo)為
與拋物線交點(diǎn)的坐標(biāo)為![]() 和
和![]() ;(2)①點(diǎn)
;(2)①點(diǎn)![]() 不在直線
不在直線![]() 上,理由詳見解析;②
上,理由詳見解析;②![]() 存在最大值,最大值為
存在最大值,最大值為![]() .
.
【解析】
(1)設(shè)拋物線解析式為y=a(x﹣2)2+4,將(0,0)代入求出a,再把![]() 代入即可解決問題;
代入即可解決問題;
(2)①由(1)中拋物線的解析式可以求出E點(diǎn)的坐標(biāo),從而可以求出ME的解析式,再將P點(diǎn)的坐標(biāo)代入直線的解析式就可以判斷P點(diǎn)是否在直線ME上.
②設(shè)出點(diǎn)N(t,﹣(t﹣2)2+4),可以表示出PN的值,根據(jù)梯形的面積公式可以表示出S與t的函數(shù)關(guān)系式,從而可以求出結(jié)論.
(1)因所求拋物線的頂點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,故可設(shè)其關(guān)系式為
,故可設(shè)其關(guān)系式為![]()
又![]() 拋物線經(jīng)過
拋物線經(jīng)過![]() ,于是得
,于是得![]() ,
,
解得![]()
![]() 所求函數(shù)關(guān)系式為
所求函數(shù)關(guān)系式為![]() ,
,
即![]()
把![]() 代入得
代入得![]()
解得:![]() ,
,![]()
![]() 直線
直線![]() 與拋物線交點(diǎn)的坐標(biāo)為
與拋物線交點(diǎn)的坐標(biāo)為![]() 和
和![]()
(2)①點(diǎn)![]() 不在直線
不在直線![]() 上.
上.
根據(jù)拋物線的對(duì)稱性可知![]() 點(diǎn)的坐標(biāo)為
點(diǎn)的坐標(biāo)為![]() ,
,
又![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,
,
設(shè)直線![]() 的關(guān)系式為
的關(guān)系式為![]()
于是得![]() ,
,
解得![]()
所以直線![]() 的關(guān)系式為
的關(guān)系式為![]() .
.
由已知條件易得,當(dāng)![]() 時(shí),
時(shí),![]() ,
,
![]()
![]() 點(diǎn)的坐標(biāo)不滿足直線
點(diǎn)的坐標(biāo)不滿足直線![]() 的關(guān)系式
的關(guān)系式![]() .
.
![]() 當(dāng)
當(dāng)![]() 時(shí),點(diǎn)
時(shí),點(diǎn)![]() 不在直線
不在直線![]() 上.
上.
②![]() 存在最大值.
存在最大值.
理由如下:
![]() 點(diǎn)
點(diǎn)![]() 在
在![]() 軸的非負(fù)半軸上,且
軸的非負(fù)半軸上,且![]() 在拋物線上,
在拋物線上,
![]() .
.
![]() 點(diǎn)
點(diǎn)![]() 的坐標(biāo)分別為
的坐標(biāo)分別為![]() 、
、![]()
![]() ,
,
![]() ,
,
![]()
(i)當(dāng)![]() ,即
,即![]() 或
或![]() 時(shí),
時(shí),
以點(diǎn)![]() 為頂點(diǎn)的多邊形是三角形,此三角形的高為
為頂點(diǎn)的多邊形是三角形,此三角形的高為![]() ,
,
![]() .
.
(ii)當(dāng)![]() 時(shí),以點(diǎn)
時(shí),以點(diǎn)![]() 為頂點(diǎn)的多邊形是四邊形.
為頂點(diǎn)的多邊形是四邊形.
![]() ,
,![]() ,
,
![]()
![]()
![]()
![]()
其中![]() ,由
,由![]() ,
,![]() ,此時(shí)
,此時(shí)![]() 最大
最大![]() .
.
綜上所述,當(dāng)![]() 時(shí),以點(diǎn)
時(shí),以點(diǎn)![]() 為頂點(diǎn)的多邊形面積有最大值,這個(gè)最大值為
為頂點(diǎn)的多邊形面積有最大值,這個(gè)最大值為![]() .
.
說明:(ii)中的關(guān)系式,當(dāng)![]() 和
和![]() 時(shí)也適合
時(shí)也適合



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
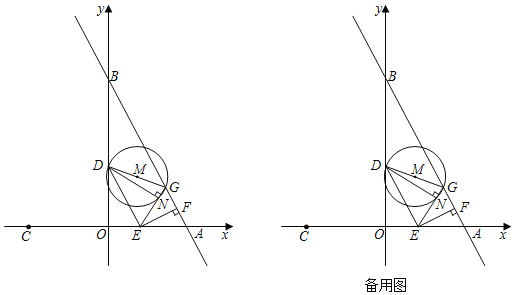
【題目】如圖,直線y=﹣2x+6與x軸,y軸分別交A,B兩點(diǎn),點(diǎn)A關(guān)于原點(diǎn)O的對(duì)稱點(diǎn)是點(diǎn)C,動(dòng)點(diǎn)E從A出發(fā)以每秒1個(gè)單位的速度運(yùn)動(dòng)到點(diǎn)C,點(diǎn)D在線段OB上滿足tan∠DEO=2,過E點(diǎn)作EF⊥AB于點(diǎn)F,點(diǎn)A關(guān)于點(diǎn)F的對(duì)稱點(diǎn)為點(diǎn)G,以DG為直徑作⊙M,設(shè)點(diǎn)E運(yùn)動(dòng)的時(shí)間為t秒;
(1)當(dāng)點(diǎn)E在線段OA上運(yùn)動(dòng),t= 時(shí),△AEF與△EDO的相似比為1:![]() ;
;
(2)當(dāng)⊙M與y軸相切時(shí),求t的值;
(3)若直線EG與⊙M交于點(diǎn)N,是否存在t使NG=![]() ,若存在,求出t的值;若不存在,說明理由.
,若存在,求出t的值;若不存在,說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
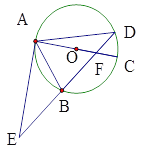
【題目】如圖,已知⊙O的直徑AC與弦BD相交于點(diǎn)F,點(diǎn)E是DB延長(zhǎng)線上的一點(diǎn),∠EAB=∠ADB;
(1)求證:AE是⊙O的切線;
(2)已知點(diǎn)B是EF的中點(diǎn),求證:△EAF∽△CBA
(3)已知AF=4,CF=2,在(2)的條件下,求AE的長(zhǎng).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系xOy中,拋物線y=mx2﹣6mx+9m+1(m≠0).
(1)求拋物線的頂點(diǎn)坐標(biāo);
(2)若拋物線與x軸的兩個(gè)交點(diǎn)分別為A和B點(diǎn)(點(diǎn)A在點(diǎn)B的左側(cè)),且AB=4,求m的值.
(3)已知四個(gè)點(diǎn)C(2,2)、D(2,0)、E(5,﹣2)、F(5,6),若拋物線與線段CD和線段EF都沒有公共點(diǎn),請(qǐng)直接寫出m的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】對(duì)于三個(gè)數(shù)a、b、c,用Ma,b,c表示這三個(gè)數(shù)的中位數(shù),用maxa,b,c表示這三個(gè)數(shù)中最大數(shù),例如:M2,1,01,max2,1,00,max2,1,a![]() 解決問題:Msin45,cos60,tan60_____,如果max3,53x,2x63,則x的取值范圍為______.
解決問題:Msin45,cos60,tan60_____,如果max3,53x,2x63,則x的取值范圍為______.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)y=-(m+2)![]() (m為常數(shù)),求當(dāng)m為何值時(shí):
(m為常數(shù)),求當(dāng)m為何值時(shí):
(1)y是x的一次函數(shù)?
(2)y是x的二次函數(shù)?并求出此時(shí)縱坐標(biāo)為-8的點(diǎn)的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖坐標(biāo)系中,O(0,0),A(3,3![]() ),B(6,0),將△OAB沿直線CD折疊,使點(diǎn)A恰好落在線段OB上的點(diǎn)E處,若OE=
),B(6,0),將△OAB沿直線CD折疊,使點(diǎn)A恰好落在線段OB上的點(diǎn)E處,若OE=![]() ,則AC:AD的值是( )
,則AC:AD的值是( )
A.1:2B.2:3C.6:7D.7:8
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】阿波羅尼奧斯(Apollonius of Perga,約公元前262-190年),古希臘數(shù)學(xué)家,與歐幾里得,阿基米德齊名,他的著作《圓錐曲線論》是古代世界光輝的科學(xué)成果.
材料:《圓錐曲線論》里面對(duì)拋物線的定義:平面內(nèi)一個(gè)動(dòng)點(diǎn)到一個(gè)定點(diǎn)與一條定直線的距離之比等于1,或者說:平面內(nèi)一動(dòng)點(diǎn)到一定點(diǎn)與一條直線的距離相等的軌跡就是拋物線.
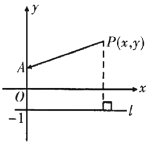
問題:已知點(diǎn)![]() ,
,![]() ,直線
,直線![]() ,連接
,連接![]() ,若點(diǎn)
,若點(diǎn)![]() 到直線
到直線![]() 的距離與
的距離與![]() 的長(zhǎng)相等,請(qǐng)求出
的長(zhǎng)相等,請(qǐng)求出![]() 與
與![]() 的關(guān)系式.
的關(guān)系式.
解:如圖,∵![]() ,
,![]() ,
,
∴![]()
∵![]() ,直線
,直線![]() ,
,
∴點(diǎn)![]() 到直線
到直線![]() 的距離為
的距離為![]()
∵點(diǎn)![]() 到直線
到直線![]() 的距離與
的距離與![]() 的長(zhǎng)相等,
的長(zhǎng)相等,
∴![]() ,
,
平方化簡(jiǎn)得,![]() .
.
若將上述問題中![]() 點(diǎn)坐標(biāo)改為
點(diǎn)坐標(biāo)改為![]() ,直線
,直線![]() 變?yōu)?/span>
變?yōu)?/span>![]() ,按照問題解題思路,試求出
,按照問題解題思路,試求出![]() 與
與![]() 的關(guān)系式,并在平面直角坐標(biāo)系中利用描點(diǎn)法畫出其圖象,你能發(fā)現(xiàn)什么?
的關(guān)系式,并在平面直角坐標(biāo)系中利用描點(diǎn)法畫出其圖象,你能發(fā)現(xiàn)什么?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某農(nóng)科所研究出一種新型的花生摘果設(shè)備,一期研發(fā)成本為每臺(tái)6萬元,該摘果機(jī)的銷售量![]() (臺(tái))與售價(jià)
(臺(tái))與售價(jià)![]() (萬元/臺(tái))之間存在函數(shù)關(guān)系:
(萬元/臺(tái))之間存在函數(shù)關(guān)系:![]() .
.
(1)設(shè)這種摘果機(jī)一期銷售的利潤(rùn)為![]() (萬元),問一期銷售時(shí),在搶占市場(chǎng)份額(提示:銷量盡可能大)的前提下利潤(rùn)達(dá)到32萬元,此時(shí)售價(jià)為多少?
(萬元),問一期銷售時(shí),在搶占市場(chǎng)份額(提示:銷量盡可能大)的前提下利潤(rùn)達(dá)到32萬元,此時(shí)售價(jià)為多少?
(2)由于環(huán)保局要求該機(jī)器必須增加除塵設(shè)備,科研所投入了7萬元研究經(jīng)費(fèi),使得環(huán)保達(dá)標(biāo)且機(jī)器的研發(fā)成本每臺(tái)降低了1萬元,若科研所的銷售戰(zhàn)略保持不變,請(qǐng)問在二期銷售中利潤(rùn)達(dá)到63萬元時(shí),該機(jī)器單臺(tái)的售價(jià)為多少?
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com