【題目】已知y＝x2＋bx＋c的圖象向右平移2個單位長度，再向下平移3個單位長度，得到的圖象對應的函數表達式為y＝x2－2x－3.
(1) 求b，c；
(2)求原函數圖象的頂點坐標；
(3)求兩個圖象頂點之間的距離．
【答案】(1)2；0；(2)頂點坐標為(－1，－1)；(3)原兩個頂點之間的距離為
.
【解析】
先把平移后的函數化為頂點式表達，再根據二次函數的平移變化得出b、c的值，即可求出相應的頂點坐標即兩頂點之間的距離.
(1)2；0
∵y＝x2－2x－3= (x-1)2-4，
此函數經過向右平移2個單位長度，再向下平移3個單位長度得到，
故平移前的函數為y＝ (x＋1)2－1，
y＝ (x＋1)2－1=y＝x2＋2x，
故a=1,b=2；
(2)原函數的表達式為y＝ (x＋1)2－1.
∴其圖象的頂點坐標為(－1，－1)．
(3)原圖象的頂點為(－1，－1)，新圖象的頂點為(1，－4)．
由勾股定理易得兩個頂點之間的距離為.
名校課堂系列答案科目：初中數學 來源： 題型：
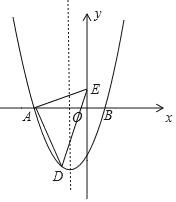
【題目】如圖，在平面直角坐標系中，二次函數y＝ax2+bx﹣3交x軸于點A（﹣3，0）、B（1，0），在y軸上有一點E（0，1），連接AE．
（1）求二次函數的表達式；
（2）若點D為拋物線在x軸負半軸下方的一個動點，求△ADE面積的最大值；
（3）拋物線對稱軸上是否存在點P，使△AEP為等腰三角形？若存在，請直接寫出所有P點的坐標；若不存在，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，O為菱形ABCD對角線上一點，以點O為圓心，OA長為半徑的⊙O與BC相切于點M．
（1）求證：CD與⊙O相切；
（2）若菱形ABCD的邊長為2，∠ABC＝60°，求⊙O的半徑．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】對于反比例函數y＝
（k≠0），下列所給的四個結論中，正確的是（ ）
A. 若點（2，4）在其圖象上，則（﹣2，4）也在其圖象上
B. 當k＞0時，y隨x的增大而減小
C. 過圖象上任一點P作x軸、y軸的垂線，垂足分別A、B，則矩形OAPB的面積為k
D. 反比例函數的圖象關于直線y＝x和y＝﹣x成軸對稱
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，P為⊙O的直徑BA延長線上的一點，PC與⊙O相切，切點為C，點D是⊙O上一點，連結PD.已知PC＝PD＝BC.下列結論：(1)PD與⊙O相切；(2)四邊形PCBD是菱形；(3)PO＝AB；(4)∠PDB＝120°.其中正確的個數為( )
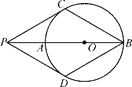
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目：初中數學 來源： 題型：
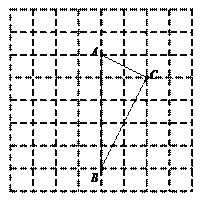
【題目】如圖，在由邊長為1的小正方形組成的網格圖中，有一個格點三角形ABC．（注：頂點均在網格線交點處的三角形稱為格點三角形．）
（1）△ABC是 三角形（填“銳角”、“直角”或“鈍角”）；
（2）若P、Q分別為線段AB、BC上的動點，當PC＋PQ取得最小值時，
① 在網格中用無刻度的直尺，畫出線段PC、PQ．（請保留作圖痕跡．）
② 直接寫出PC＋PQ的最小值： .
查看答案和解析>>
科目：初中數學 來源： 題型：
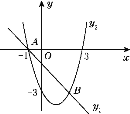
【題目】如圖，A(－1，0)，B(2，－3)兩點在一次函數y＝－x＋m與二次函數y＝ax2＋bx－3的圖象上．
(1)求m的值和二次函數的表達式；
(2)設二次函數的圖象交y軸于點C，求△ABC的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（2013年四川綿陽12分）如圖，已知矩形OABC中，OA=2，AB=4，雙曲線
（k＞0）與矩形兩邊AB、BC分別交于E、F．
（1）若E是AB的中點，求F點的坐標；
（2）若將△BEF沿直線EF對折，B點落在x軸上的D點，作EG⊥OC，垂足為G，證明△EGD∽△DCF，并求k的值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
