
【題目】如圖,在Rt△ABC中,∠A=90°,AB=6,AC=8,D,E分別是邊AB,AC的中點,點P從點D出發沿DE方向運動,過點P作PQ⊥BC于Q,過點Q作QR∥BA交AC于R,當點Q與點C重合時,點P停止運動.設BQ=x,QR=y.
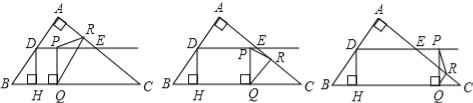
(1)求點D到BC的距離DH的長;
(2)求y關于x的函數關系式(不要求寫出自變量的取值范圍);
(3)是否存在點P,使△PQR為等腰三角形?若存在,請求出所有滿足要求的x的值;若不存在,請說明理由.
【答案】(1)![]() (2)y=-
(2)y=-![]() x+6(3)存在,
x+6(3)存在,![]() 或6或
或6或![]()
【解析】
試題分析:(1)根據三角形相似的判定定理求出△BHD∽△BAC,根據相似三角形的性質求出DH的長;
(2)根據△RQC∽△ABC,根據三角形的相似比求出y關于x的函數關系式;
(3)畫出圖形,根據圖形進行討論:
①當PQ=PR時,過點P作PM⊥QR于M,則QM=RM.由于∠1+∠2=90°,∠C+∠2=90°,∴∠1=∠C.
∴cos∠1=cosC=![]() ,∴
,∴![]() ,即可求出x的值;
,即可求出x的值;
②當PQ=RQ時,﹣![]() x+6=
x+6=![]() ,x=6;
,x=6;
③當PR=QR時,則R為PQ中垂線上的點,于是點R為EC的中點,故CR=![]() CE=
CE=![]() AC=2.由于tanC=
AC=2.由于tanC=![]() ,x=
,x=![]() .
.
試題解析:(1)在Rt△ABC中,
∵∠A=90°,AB=6,AC=8,
∴BC=![]() =10.
=10.
∵∠DHB=∠A=90°,∠B=∠B.
∴△BHD∽△BAC,
∴![]() ,
,
∴DH=![]() AC=
AC=![]() ×8=
×8=![]()
(2)∵QR∥AB,
∴∠QRC=∠A=90°.
∵∠C=∠C,
∴△RQC∽△ABC,
∴![]() ,∴
,∴![]() ,
,
即y關于x的函數關系式為:y=-![]() x+6.
x+6.
(3)存在,分三種情況:
①當PQ=PR時,過點P作PM⊥QR于M,則QM=RM.
∵∠1+∠2=90°,∠C+∠2=90°,
∴∠1=∠C.
∴cos∠1=cosC=![]() ,
,
∴![]() ,
,
∴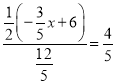 ,
,
∴x=![]() .
.
②當PQ=RQ時,﹣![]() x+6=
x+6=![]() ,
,
∴x=6.
③作EM⊥BC,RN⊥EM,
∴EM∥PQ,
當PR=QR時,則R為PQ中垂線上的點,
∴EN=MN,
∴ER=RC,
∴點R為EC的中點,
∴CR=![]() CE=
CE=![]() AC=2.
AC=2.
∵tanC=![]() ,
,
∴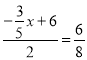 ,
,
∴x=![]() .
.
綜上所述,當x為![]() 或6或
或6或![]() 時,△PQR為等腰三角形.
時,△PQR為等腰三角形.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】已知二次函數y=mx2+nx+p圖象的頂點橫坐標是2,與x軸交于A(x1,0)、B(x2,0),x1<0<x2,與y軸交于點C,O為坐標原點,tan∠CAO﹣tan∠CBO=1.
(1)求證:n+4m=0;
(2)求m、n的值;
(3)當p>0且二次函數圖象與直線y=x+3僅有一個交點時,求二次函數的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】關于一組數據的平均數、中位數、眾數,下列說法中正確的是:
A. 平均數一定是這組數中的某個數 B. 眾數一定是這組數中的某個數
C. 中位數一定是這組數中的某個數 D. 以上說法都不對
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某自然保護區的面積為2150 000 000平方米,2150000000這個數用科學計數法表示為:
A. 2.15×108 B. 21.5×108 C. 2.15×109 D. 0.215×109
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列命題中錯誤的有( )個
(1)等腰三角形的兩個底角相等
(2)對角線相等且互相垂直的四邊形是正方形
(3)對角線相等的四邊形為矩形
(4)圓的切線垂直于半徑
(5)平分弦的直徑垂直于弦
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】根據下列條件可列出一元一次方程的是( )
A. a與1的和的3倍
B. 甲數的2倍與乙數的3倍的和
C. a與b的差的20%
D. 一個數的3倍是5
查看答案和解析>>
科目:初中數學 來源: 題型:
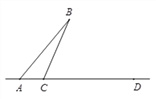
【題目】如圖,線段AB,AD交于點A.C為直線AD上一點(不與點A,D重合).過點C在BC的右側作射線CE⊥BC,過點D作直線DF∥AB,交CE于點G(G與D不重合).
(1)如圖1,若點C在線段AD上,且∠BCA為鈍角.
①按要求補全圖形;②判斷∠B與∠CGD的數量關系,并證明.
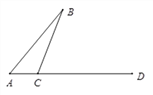
(2)若點C在線段DA的延長線上,請直接寫出∠B與∠CGD的數量關系 ;
附加題(2分).
請你結合28題的題意提出一個新的拓展問題 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com