【題目】如圖，已知△ABC和△DEF，點E在BC邊上，點A在DE邊上，邊EF和邊AC相交于點G．如果AE=EC，∠AEG=∠B，那么添加下列一個條件后，仍無法判定△DEF與△ABC一定相似的是（ ） 
A.
= 
B.
= 
C.
= 
D.
= 
【答案】C
【解析】解：當 
= 
時，則 
= 
，而∠B=∠AEG，所以△ABC∽△EDF； 當 
= 
，則 
= 
，而∠DEF=∠AEG，所以△DEF∽△AEG，又因為AE=EC，所以∠EAG=∠C，而∠AEG=∠B，所以△AEG∽△ABC，所以△ABC∽△EDF；
當 
= 
，則 = ，而∠DEF=∠AEG，所以△DEF∽△AEG，又因為AE=EC，所以∠EAG=∠C，而∠AEG=∠B，所以△AEG∽△ABC，所以△ABC∽△EDF．
故選C．
【考點精析】解答此題的關鍵在于理解相似三角形的判定的相關知識，掌握相似三角形的判定方法:兩角對應相等，兩三角形相似（ASA）；直角三角形被斜邊上的高分成的兩個直角三角形和原三角形相似； 兩邊對應成比例且夾角相等，兩三角形相似（SAS）；三邊對應成比例，兩三角形相似（SSS）．
科目：初中數學 來源： 題型：
【題目】如果一次函數
的圖象與
軸交點坐標為
，如圖所示．則下列說法：①
隨的增大而減小；②關于的方程
的解為
；③
的解是
；④
．其中正確的說法有_____．（只填你認為正確說法的序號）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知拋物線
與
軸交于
和
兩點，與
軸交于
點．
（1）求此拋物線的解析式；
（2）設
是線段
上的動點，作
交
于
，連接
，當
的面積是
面積的2倍時，求點的坐標；
（3）若
為拋物線上
、兩點間的一個動點，過作軸的平行線，交
于
，當點運動到什么位置時，線段
的值最大，并求此時點的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，AB=8cm，BC=16cm，點P從點A出發沿AB邊想向點B以2cm/s的速度移動，點Q從點B出發沿BC邊向點C以4cm/s的速度移動，如果P、Q同時出發，經過幾秒后△PBQ和△ABC相似？ 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，AB＝AC，∠BAC＝50°，∠BAC的平分線與AB的中垂線交于點O，點C沿EF折疊后與點O重合，則∠CEO的度數是_____．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在Rt△ABC中，AC＝BC，點D為AB中點．∠GDH＝90°，∠GDH繞點D旋轉，DG，DH分別與邊AC，BC交于E，F兩點．下列結論：①AE+BF＝AC，②AE2+BF2＝EF2，③S四邊形CEDF＝
S△ABC，④△DEF始終為等腰直角三角形．其中正確的是( )
A. ①②③④ B. ①②③ C. ①④ D. ②③
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，AB≠AC．D、E分別為邊AB、AC上的點．AC=3AD，AB=3AE，點F為BC邊上一點，添加一個條件： ， 可以使得△FDB與△ADE相似．（只需寫出一個） 
查看答案和解析>>
科目：初中數學 來源： 題型：
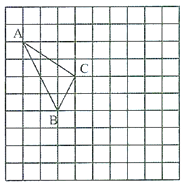
【題目】在如圖所示的正方形網格中，每個小正方形的邊長為1，格點三角形△ABC的頂點A、C的坐標分別為(－4，5)，(－1，3).
（1）請在如圖所示的網格平面內作出平面直角坐標系；
（2）請把△ABC先向右移動5個單位，再向下平移3個單位得到△
，在圖中畫出△；
（3）求△ABC的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
