
【題目】閱讀理解:在平面直角坐標(biāo)系中,若兩點(diǎn)P、Q的坐標(biāo)分別是P(x1,y1)、
Q(x2,y2),則P、Q這兩點(diǎn)間的距離為|PQ|=![]() .如P(1,2),Q(3,4),則|PQ|=
.如P(1,2),Q(3,4),則|PQ|=![]() =2
=2![]() .
.
對(duì)于某種幾何圖形給出如下定義:符合一定條件的動(dòng)點(diǎn)形成的圖形,叫做符合這個(gè)條件的點(diǎn)的軌跡.如平面內(nèi)到線段兩個(gè)端點(diǎn)距離相等的點(diǎn)的軌跡是這條線段的垂直平分線.
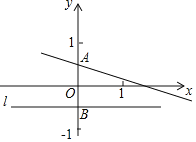
解決問題:如圖,已知在平面直角坐標(biāo)系xOy中,直線y=kx+![]() 交y軸于點(diǎn)A,點(diǎn)A關(guān)于x軸的對(duì)稱點(diǎn)為點(diǎn)B,過點(diǎn)B作直線l平行于x軸.
交y軸于點(diǎn)A,點(diǎn)A關(guān)于x軸的對(duì)稱點(diǎn)為點(diǎn)B,過點(diǎn)B作直線l平行于x軸.
(1)到點(diǎn)A的距離等于線段AB長(zhǎng)度的點(diǎn)的軌跡是 ;
(2)若動(dòng)點(diǎn)C(x,y)滿足到直線l的距離等于線段CA的長(zhǎng)度,求動(dòng)點(diǎn)C軌跡的函數(shù)表達(dá)式;
問題拓展:(3)若(2)中的動(dòng)點(diǎn)C的軌跡與直線y=kx+![]() 交于E、F兩點(diǎn),分別過E、F作直線l的垂線,垂足分別是M、N,求證:①EF是△AMN外接圓的切線;②
交于E、F兩點(diǎn),分別過E、F作直線l的垂線,垂足分別是M、N,求證:①EF是△AMN外接圓的切線;②![]() 為定值.
為定值.
【答案】(1)x2+(y﹣![]() )2=1;(2)動(dòng)點(diǎn)C軌跡的函數(shù)表達(dá)式y=
)2=1;(2)動(dòng)點(diǎn)C軌跡的函數(shù)表達(dá)式y=![]() x2;(3)①證明見解析;②證明見解析.
x2;(3)①證明見解析;②證明見解析.
【解析】
(1)利用兩點(diǎn)間的距離公式即可得出結(jié)論;
(2)利用兩點(diǎn)間的距離公式即可得出結(jié)論;
(3)①先確定出m+n=2k,mn=﹣1,再確定出M(m,﹣![]() ),N(n,﹣
),N(n,﹣![]() ),進(jìn)而判斷出△AMN是直角三角形,再求出直線AQ的解析式為y=﹣
),進(jìn)而判斷出△AMN是直角三角形,再求出直線AQ的解析式為y=﹣![]() x+
x+![]() ,即可得出結(jié)論;
,即可得出結(jié)論;
②先確定出a=mk+![]() ,b=nk+
,b=nk+![]() ,再求出AE=ME=a+
,再求出AE=ME=a+![]() =mk+1,AF=NF=b+
=mk+1,AF=NF=b+![]() =nk+1,即可得出結(jié)論.
=nk+1,即可得出結(jié)論.
(1)設(shè)到點(diǎn)A的距離等于線段AB長(zhǎng)度的點(diǎn)D坐標(biāo)為(x,y),
∴AD2=x2+(y﹣![]() )2,
)2,
∵直線y=kx+![]() 交y軸于點(diǎn)A,
交y軸于點(diǎn)A,
∴A(0,![]() ),
),
∵點(diǎn)A關(guān)于x軸的對(duì)稱點(diǎn)為點(diǎn)B,
∴B(0,﹣![]() ),
),
∴AB=1,
∵點(diǎn)D到點(diǎn)A的距離等于線段AB長(zhǎng)度,
∴x2+(y﹣![]() )2=1,
)2=1,
故答案為:x2+(y﹣![]() )2=1;
)2=1;
(2)∵過點(diǎn)B作直線l平行于x軸,
∴直線l的解析式為y=﹣![]() ,
,
∵C(x,y),A(0,![]() ),
),
∴AC2=x2+(y﹣![]() )2,點(diǎn)C到直線l的距離為:(y+
)2,點(diǎn)C到直線l的距離為:(y+![]() ),
),
∵動(dòng)點(diǎn)C(x,y)滿足到直線l的距離等于線段CA的長(zhǎng)度,
∴x2+(y﹣![]() )2=(y+
)2=(y+![]() )2,
)2,
∴動(dòng)點(diǎn)C軌跡的函數(shù)表達(dá)式y=![]() x2;
x2;
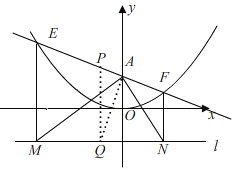
(3)①如圖,
設(shè)點(diǎn)E(m,a)點(diǎn)F(n,b),
∵動(dòng)點(diǎn)C的軌跡與直線y=kx+![]() 交于E、F兩點(diǎn),
交于E、F兩點(diǎn),
∴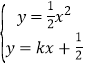 ,
,
∴x2﹣2kx﹣1=0,
∴m+n=2k,mn=﹣1,
∵過E、F作直線l的垂線,垂足分別是M、N,
∴M(m,﹣![]() ),N(n,﹣
),N(n,﹣![]() ),
),
∵A(0,![]() ),
),
∴AM2+AN2=m2+1+n2+1=m2+n2+2=(m+n)2﹣2mn+2=4k2+4,
MN2=(m﹣n)2=(m+n)2﹣4mn=4k2+4,
∴AM2+AN2=MN2,
∴△AMN是直角三角形,MN為斜邊,
取MN的中點(diǎn)Q,
∴點(diǎn)Q是△AMN的外接圓的圓心,
∴Q(k,﹣![]() ),
),
∵A(0,![]() ),
),
∴直線AQ的解析式為y=﹣![]() x+
x+![]() ,
,
∵直線EF的解析式為y=kx+![]() ,
,
∴AQ⊥EF,
∴EF是△AMN外接圓的切線;
②∵點(diǎn)E(m,a)點(diǎn)F(n,b)在直線y=kx+![]() 上,
上,
∴a=mk+![]() ,b=nk+
,b=nk+![]() ,
,
∵ME,NF,EF是△AMN的外接圓的切線,
∴AE=ME=a+![]() =mk+1,AF=NF=b+
=mk+1,AF=NF=b+![]() =nk+1,
=nk+1,
∴![]() =
=![]() =2,
=2,
即:![]() 為定值,定值為2.
為定值,定值為2.


 小學(xué)期末沖刺100分系列答案
小學(xué)期末沖刺100分系列答案 期末復(fù)習(xí)檢測(cè)系列答案
期末復(fù)習(xí)檢測(cè)系列答案 超能學(xué)典單元期中期末專題沖刺100分系列答案
超能學(xué)典單元期中期末專題沖刺100分系列答案 黃岡360度定制密卷系列答案
黃岡360度定制密卷系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】下列有四個(gè)結(jié)論:①若![]() ,則
,則![]() ;
;
②若![]() ,
,![]() ,則
,則![]() 的值為
的值為![]() ;
;
③若![]() 的運(yùn)算結(jié)果中不含
的運(yùn)算結(jié)果中不含![]() 項(xiàng),則
項(xiàng),則![]() ;
;
④若![]() ,
,![]() ,則
,則![]() 可表示為
可表示為![]() .
.
其中正確的是(填序號(hào))是:______.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
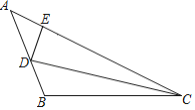
【題目】如圖,在△ABC中,∠B>90°,CD為∠ACB的角平分線,在AC邊上取點(diǎn)E,使DE=DB,且∠AED>90°.若∠A=α,∠ACB=β,則( )
A.∠AED=180°﹣α﹣βB.∠AED=180°﹣α﹣![]() β
β
C.∠AED=90°﹣α+βD.∠AED=90°+α+![]() β
β
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
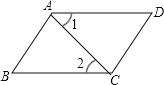
【題目】 根據(jù)題意,完成推理填空:如圖,AB∥CD,∠1=∠2,試說明∠B=∠D.
解:∵∠1=∠2(已知)
∴ (內(nèi)錯(cuò)角相等,兩直線平行)
∴∠BAD+∠B=180°(兩直線平行,同旁內(nèi)角互補(bǔ))
∵AB∥CD
∴ + =180°,
∴∠B=∠D
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知一次函數(shù)![]() ,其中
,其中![]() .
.
(1)若點(diǎn)![]() 在y1的圖象上.求a的值:
在y1的圖象上.求a的值:
(2)當(dāng)![]() 時(shí).若函數(shù)有最大值2.求y1的函數(shù)表達(dá)式;
時(shí).若函數(shù)有最大值2.求y1的函數(shù)表達(dá)式;
(3)對(duì)于一次函數(shù)![]() ,其中
,其中![]() ,若對(duì)- -切實(shí)數(shù)x,
,若對(duì)- -切實(shí)數(shù)x,![]() 都成立,求a,m需滿足的數(shù)量關(guān)系及 a的取值范圍.
都成立,求a,m需滿足的數(shù)量關(guān)系及 a的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
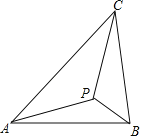
【題目】(2017湖南株洲)如圖示,若△ABC內(nèi)一點(diǎn)P滿足∠PAC=∠PBA=∠PCB,則點(diǎn)P為△ABC的布洛卡點(diǎn).三角形的布洛卡點(diǎn)(Brocard point)是法國數(shù)學(xué)家和數(shù)學(xué)教育家克洛爾(A.L.Crelle 1780﹣1855)于1816年首次發(fā)現(xiàn),但他的發(fā)現(xiàn)并未被當(dāng)時(shí)的人們所注意,1875年,布洛卡點(diǎn)被一個(gè)數(shù)學(xué)愛好者法國軍官布洛卡(Brocard 1845﹣1922)重新發(fā)現(xiàn),并用他的名字命名.問題:已知在等腰直角三角形DEF中,∠EDF=90°,若點(diǎn)Q為△DEF的布洛卡點(diǎn),DQ=1,則EQ+FQ=( )
A. 5 B. 4 C. 3+![]() D. 2+
D. 2+![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
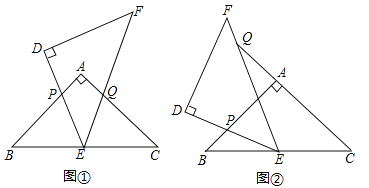
【題目】(2017甘肅省天水市)△ABC和△DEF是兩個(gè)全等的等腰直角三角形,∠BAC=∠EDF=90°,△DEF的頂點(diǎn)E與△ABC的斜邊BC的中點(diǎn)重合,將△DEF繞點(diǎn)E旋轉(zhuǎn),旋轉(zhuǎn)過程中,線段DE與線段AB相交于點(diǎn)P,線段EF與射線CA相交于點(diǎn)Q.
(1)如圖①,當(dāng)點(diǎn)Q在線段AC上,且AP=AQ時(shí),求證:△BPE≌△CQE;
(2)如圖②,當(dāng)點(diǎn)Q在線段CA的延長(zhǎng)線上時(shí),求證:△BPE∽△CEQ;并求當(dāng)BP=2,CQ=9時(shí)BC的長(zhǎng).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,四邊形ABCD為平行四邊形紙片.把紙片ABCD折疊,使點(diǎn)B恰好落在CD邊上,折痕為AF.且AB=10cm、AD=8cm、DE=6cm.
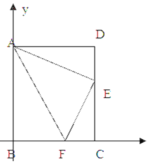
(1)求證:平行四邊形ABCD是矩形;
(2)如圖2,以點(diǎn)B為坐標(biāo)原點(diǎn),水平方向、豎直方向?yàn)?/span>x軸、y軸建立平面直角坐標(biāo)系,求直線AF的解析式;
(3)在(2)中的坐標(biāo)系內(nèi)是否存在這樣的點(diǎn)P,使得以點(diǎn)P、A、E、F為頂點(diǎn)的四邊形是平行四邊形?若不存在,請(qǐng)說明理由;若存在,直接寫出點(diǎn)P的坐標(biāo)。
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com