
【題目】如圖,AD為△ABC的中線,BE為△ABD的中線.
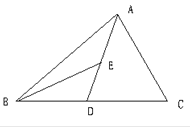
(1)∠ABE=15°,∠BAD=40°,求∠BED的度數;
(2)在△BED中作BD邊上的高;
(3)若△ABC的面積為40,BD=5,則△BDE 中BD邊上的高為多少?
【答案】(1)55°;(2)作圖見解析;(3)4.
【解析】
(1)根據三角形內角與外角的性質解答即可;
(2)過E作BC邊的垂線即可;
(3)過A作BC邊的垂線AG,再根據三角形中位線定理求解即可.
解:(1)∵∠BED是△ABE的外角,
∴∠BED=∠ABE+∠BAD=15°+40°=55°;
(2)過E作BC邊的垂線,F為垂足,則EF為所求;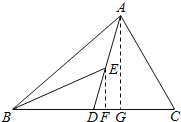
(3)過A作BC邊的垂線AG,
∴AD為△ABC的中線,BD=5,
∴BC=2BD=2×5=10,
∵△ABC的面積為40,
∴![]() BCAG=40,即
BCAG=40,即![]() ×10AG=40,解得AG=8,
×10AG=40,解得AG=8,
∵EF⊥BC于F,
∴EF∥AG,
∵E為AD的中點,
∴EF是△AGD的中位線,
∴EF=![]() AG=
AG=![]() ×8=4.
×8=4.


 每課必練系列答案
每課必練系列答案 巧學巧練系列答案
巧學巧練系列答案科目:初中數學 來源: 題型:
【題目】兩幢大樓的部分截面及相關數據如圖,小明在甲樓A處透過窗戶E發現乙樓F處出現火災,此時A,E,F在同一直線上.跑到一樓時,消防員正在進行噴水滅火,水流路線呈拋物線,在1.2m高的D處噴出,水流正好經過E,F. 若點B和點E、點C和F的離地高度分別相同,現消防員將水流拋物線向上平移0.4m,再向左后退了____m,恰好把水噴到F處進行滅火.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖(1)是某河上一座古拱橋的截面圖,拱橋橋洞上沿是拋物線形狀,拋物線兩端點與水面的距離都是1m,拱橋的跨度為10m,橋洞與水面的最大距離是5m,橋洞兩側壁上各有一盞距離水面4m的景觀燈.現把拱橋的截面圖放在平面直角坐標系中,如圖(2).


求(1)拋物線的解析式;
(2)兩盞景觀燈P1、P2之間的水平距離.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2+bx+c的圖象如圖所示,它與x軸的兩個交點分別為(-1,0),(3,0).對于下列命題:①b-2a=0;②abc<0;③a-2b+4c<0;④8a+c>0.其中正確的有____________。

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,設一個三角形的三邊分別是3,13m,8.

(1)求m的取值范圍;
(2)是否存在整數m使三角形的周長為偶數?若存在,求出三角形的周長;若不存在,說明理由;
(3)如圖,在(2)的條件下,當AB=8,AC=13m,BC=3時,若D是AB的中點,連CD,P是CD上動點(不與C,D重合,當P在線段CD上運動時,有兩個式子):①![]() ;②
;②![]() ,其中有一個的值不變,另一個的值改變。問題:
,其中有一個的值不變,另一個的值改變。問題:
A.請判斷出誰不變,誰改變;
B.若不變的求出其值,若改變的求出變化的范圍。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列文字:我們知道對于一個圖形,通過不同的方法計算圖形的面積,可以得到一個數學等式,例如由圖1可以得到(a+2b)(a+b)= a2+3ab+2b2.請解答下列問題:
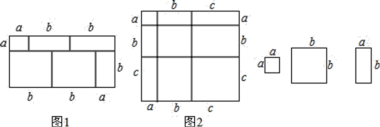
(1)寫出圖2中所表示的數學等式 ;
(2)利用(1)中所得到的結論,解決下面的問題:已知a+b+c=9,ab+bc+ac=29,求a 2+b2+c2的值;
(3)小明同學打算用x張邊長為a和y張邊長為b的小正方形,z張相鄰兩邊長分別為a、b的長方形紙片拼出了一個面積為(3a+5b)(4a+7b)的長方形,那么他總共需要多少張紙片?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,平面直角坐標系中,矩形OABC的邊與函數y=![]() (x>0)圖象交于E,F兩點,且F是BC的中點,則四邊形ACFE的面積等于( )
(x>0)圖象交于E,F兩點,且F是BC的中點,則四邊形ACFE的面積等于( )
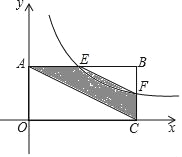
A. 4 B. 6 C. 8 D. 不能確定
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com