
【題目】如圖,在△ABC中,∠ABC=90°,過點B作BD⊥AC于點D,BE平分∠ABD交AC于點E.

(1)求證:CB=CE;
(2)若∠CEB=80°,求∠DBC的大小.
【答案】(1)證明見詳解,(2)∠DBC =70°.
【解析】
(1)由BD⊥AC結合∠ABC=90°可證明∠A+∠C=90°,∠DBC+∠C=90°,由BE平分∠ABD得∠ABE=∠DBE,由∠CBE=∠CBD+∠DBE,∠CEB=∠A+∠ABE證得∠CBE=∠CEB即可.
(2)利用等腰三角形的性質求出∠C即可解決問題.
(1)證明:∵BD⊥AC,
∴∠CDB=90°,
∵∠ABC=90°,
∴∠A+∠C=90°,∠DBC+∠C=90°,
∵BE平分∠ABD,
∴∠ABE=∠DBE,
∵∠CBE=∠CBD+∠DBE,∠CEB=∠A+∠ABE,
∴∠CBE=∠CEB,
∴CB=CE.
(2)∵∠CEB=∠CBE=80°,
∴∠C=180°-2×80°=20°,
∵∠CDB=90°,
∴∠DBC=90°-20°=70°.


科目:初中數學 來源: 題型:
【題目】小華有一個容量為8GB (1GB= 1024MB)的U盤,U盤中已經存儲了一個視頻文件,其余空間都用來存儲照片,若每張照片占用的內存容量均相同,圖片數量x (張)和剩余可用空間y (MB)的部分關系如表:
圖片數量 | 100 | 150 | 200 | 400 | 800 |
剩余可用空間 | 5700 | 5550 | 5400 | 4800 | 3600 |
(1)由上表可知,y與x之間滿足___ ___(填“一次”或“二次”或“反比例”)函數的關系,求出y與x之間的關系式.
(2)求出U盤中視頻文件的占用內存容量.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有A、B兩個港口,水由A流向B,水流的速度是4千米/小時,甲、乙兩船同時由A順流駛向B,各自不停地在A、B之間往返航行,甲在靜水中的速度是28千米/小時,乙在靜水中的速度是20千米/小時.

設甲行駛的時間為t小時,甲船距B港口的距離為S1千米,乙船距B港口的距離為S2千米,如圖為S1(千米)和t(小時)函數關系的部分圖象.
(1)A、B兩港口距離是_____千米.
(2)在圖中畫出乙船從出發到第一次返回A港口這段時間內,S2(千米)和t(小時)的函數關系的圖象.
(3)求甲、乙兩船第二次(不算開始時甲、乙在A處的那一次)相遇點M位于A、B港口的什么位置?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,分別以直角三角形的三邊為邊長向外作正方形,然后分別以三個正方形的中心為圓心,正方形邊長的一半為半徑作圓,記三個圓的面積分別為![]() ,
,![]() ,
,![]() ,則
,則![]() ,
,![]() ,
,![]() 之間的關系是( )
之間的關系是( )

A.![]() B.
B.![]() C.
C.![]() D.無法確定
D.無法確定
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在已知的△ABC中,按以下步驟作圖:①分別以B、C為圓心,以大于![]() BC的長為半徑作弧,兩弧相交于點M、N;②作直線MN交AB于點D,連接CD,若CD=AD,∠B=20°,則下列結論中錯誤的是( )
BC的長為半徑作弧,兩弧相交于點M、N;②作直線MN交AB于點D,連接CD,若CD=AD,∠B=20°,則下列結論中錯誤的是( )

A. ∠CAD=40° B. ∠ACD=70° C. 點D為△ABC的外心 D. ∠ACB=90°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,等腰Rt△ABC中,∠ACB=90°,AC=BC,點D、E分別在邊AB、CB上,CD=DE,∠CDB=∠DEC,過點C作CF⊥DE于點F,交AB于點G,
(1)求證:△ACD≌△BDE;
(2)求證:△CDG為等腰三角形.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2018年5月12日是我國第十個全國防災減災日,也是汶川地震十周年.為了弘揚防災減災文化,普及防災減災知識和技能,鄭州W中學通過學校安全教育平臺號召全校學生進行學習,并對學生學習成果進行了隨機抽取,現對部分學生成績(x為整數,滿分100分)進行統計.繪制了如圖尚不完整的統計圖表:
調查結果統計表
組別 | 分數段 | 頻數 |
A | 50≤x<60 | a |
B | 60≤x<70 | 80 |
C | 70≤x<80 | 100 |
D | 80≤x<90 | 150 |
E | 90≤x<100 | 120 |
合計 | b |
根據以上信息解答下列問題:
(1)填空:a= ,b= ;
(2)扇形統計圖中,m的值為 ,“D”所對應的圓心角的度數是 度;
(3)本次調查測試成績的中位數落在 組內;
(4)若參加學習的同學共有2000人,請你估計成績在90分及以上的同學大約有多少人?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校數學興趣小組進行戶外興趣活動:測量河中橋墩露出水面部分AB的高度.如圖所示,在點C處測得∠BCA=45°.在坡比為i=1:3,高度DE=15米的小山坡頂E處測得橋墩頂部B的仰角為20°,則橋墩露出水面部分AB的高度約為(精確到1米,參考數據:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)( )

A. 34 B. 48 C. 49 D. 64
查看答案和解析>>
科目:初中數學 來源: 題型:
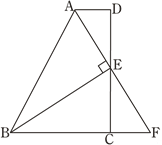
【題目】如圖,在四邊形ABCD中,AD∥BC,E為CD的中點,連接AE、BE,BE⊥AE,延長AE交BC的延長線于點F. 已知AD=2cm,BC=5cm.
(1)求證:FC=AD;
(2)求AB的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com