【題目】如圖，已知一次函數與反比例函數的圖象交于點A（﹣4，﹣2）和B（a，4）．
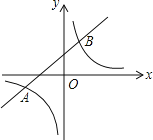
（1）求一次函數和反比例函數的表達式及點B的坐標；
（2）根據圖象回答，當x在什么范圍內時，一次函數的值大于反比例函數．
【答案】（1）一次函數表達式為y=x+2；反比例函數的解析式為y=
．點B的坐標為B（2，4）；（2）當x＞2或﹣4＜x＜0時，一次函數的值大于反比例函數的值．
【解析】
試題分析：（1）設反比例函數的解析式為y=
（k≠0），把A點坐標代入即可得出k的值，進而得出反比例函數的解析式，再把B點坐標代入即可得出a的值，利用待定系數法即可得出一次函數的解析式；
（2）直接根據兩函數的交點即可得出結論．
解：（1）設反比例函數的解析式為y=（k≠0），
∵反比例函數圖象經過點A（﹣4，﹣2），
∴﹣2=
，解得k=8，
∴反比例函數的解析式為y=．
∵B（a，4）在y=的圖象上，
∴4=
，
∴a=2，
∴點B的坐標為B（2，4）；
設一次函數表達式為y=mx+n，將點A，點B代入得，
，解得
，
∴一次函數表達式為y=x+2；
（2）根據圖象得，當x＞2或﹣4＜x＜0時，一次函數的值大于反比例函數的值．
科目：初中數學 來源： 題型：
【題目】在平面直角坐標系xOy中，已知拋物線y=﹣
+c與x軸交于A、B兩點（點A在點B的左側），交y軸的正半軸于點C，其頂點為M，MH⊥x軸于點H，MA交y軸于點N，sin∠MOH=
．
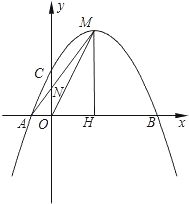
（1）求此拋物線的函數表達式；
（2）過H的直線與y軸相交于點P，過O，M兩點作直線PH的垂線，垂足分別為E，F，若
=
時，求點P的坐標；
（3）將（1）中的拋物線沿y軸折疊，使點A落在點D處，連接MD，Q為（1）中的拋物線上的一動點，直線NQ交x軸于點G，當Q點在拋物線上運動時，是否存在點Q，使△ANG與△ADM相似？若存在，求出所有符合條件的直線QG的解析式；若不存在，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】超市有一種“喜之郎”果凍禮盒，內裝兩個上下倒置的果凍，果凍高為4cm，底面是個直徑為6cm的圓，橫截面可以近似地看作一個拋物線，為了節省成本，包裝應盡可能的小，那么要制作這樣一個包裝盒至少紙板（ ）平方厘米．（不計重合部分）
A．253 B．288 C．206 D．245
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】我省2013年的快遞業務量為1.4億件，受益于電子商務發展和法治環境改善等多重因素，快遞業務迅猛發展，2014年增速位居全國第一．若2015年的快遞業務量達到4.5億件，設2014年與2015年這兩年的平均增長率為x，則下列方程正確的是( )
A. 1.4(1＋x)＝4.5 B. 1.4(1＋2x)＝4.5
C. 1.4(1＋x)2＝4.5 D. 1.4(1＋x)＋1.4(1＋x)2＝4.5
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
