
【題目】利用圖象解一元二次方程x2-2x-1=0時,我們采用的一種方法是在直角坐標系中畫出拋物線y=x2和直線y=2x+1,兩圖象交點的橫坐標就是該方程的解.
(1)請再給出一種利用圖象求方程x2-2x-1=0的解的方法;
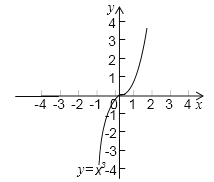
(2)已知函數y=x3的圖象(如圖),求方程x3-x-2=0的解(結果保留兩位有效數字).
 奪冠金卷全能練考系列答案
奪冠金卷全能練考系列答案科目:初中數學 來源: 題型:
【題目】如圖,一次函數y=﹣2x+4的圖象與x軸、y軸分別交于點A、B,點C是OA的中點,過點C作CD⊥OA于C交一次函數圖象于點D,P是OB上一動點,則PC+PD的最小值為( )

A.4B.![]() C.2
C.2![]() D.2
D.2![]() +2
+2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】請閱讀下述材料:
下述形式的繁分數叫做有限連分數,其中n是自然數,a0是整數,a1,a2,a3,…,an是正整數:

其中![]() 稱為部分商。
稱為部分商。
按照以下方式可將任何一個分數轉化為連分數的形式:![]() ,則
,則![]() ;考慮
;考慮![]() 的倒數,有
的倒數,有![]() ,從而
,從而 ;再考慮
;再考慮![]() 的倒數,有
的倒數,有![]() ,于是得到a的連分數展開式,它有4個部分商:3,1,3,3;
,于是得到a的連分數展開式,它有4個部分商:3,1,3,3;

可利用連分數來求二元一次不定方程的特殊解,以![]() 為例,首先將
為例,首先將![]() 寫成連分數的形式,如上所示;其次,數部分商的個數,本例是偶數個部分商(奇數情況請見下例);最后計算倒數第二個漸近分數
寫成連分數的形式,如上所示;其次,數部分商的個數,本例是偶數個部分商(奇數情況請見下例);最后計算倒數第二個漸近分數 ,從而
,從而![]() 是一個特解。
是一個特解。
考慮不定方程![]() ,先將
,先將![]() 寫成連分數的形式:
寫成連分數的形式: 。
。
注意到此連分數有奇數個部分商,將之改寫為偶數個部分商的形式:

計算倒數第二個漸近分數: ,所以
,所以![]() 是
是![]() 的一個特解。
的一個特解。
對于分式,有類似的連分式的概念,利用將分數展開為連分數的方法,可以將分式展開為連分式。例如![]() 的連分式展開式如下,它有3個部分商:
的連分式展開式如下,它有3個部分商:![]()
![]() ;
;

再例如, ,它有4個部分商:1,
,它有4個部分商:1,![]() 。
。
請閱讀上述材料,利用所講述的方法,解決下述兩個問題
(1)找出兩個關于x的多項式p和q,使得![]() 。
。
(2)找出兩個關于x的多項式u和v,使得![]() 。
。
查看答案和解析>>
科目:初中數學 來源: 題型:
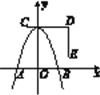
【題目】如圖,一條拋物線與x軸相交于A,B兩點,其頂點P在折線C-D-E上移動,若點C,D,E的坐標分別為(-1,4),(3,4),(3,1),點B的橫坐標的最小值為1,則點A的橫坐標的最大值為________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在數軸上![]() 點表示數
點表示數![]() ,
,![]() 點表示數
點表示數![]() ,
,![]() 點表示數
點表示數![]() ,已知數
,已知數![]() 是最小的正整數,且
是最小的正整數,且![]() 、
、![]() 滿足
滿足![]() .
.
![]()
(1)![]() ,
,![]() ,
,![]() ;
;
(2)若將數軸折疊,使得點![]() 與點
與點![]() 重合,則點
重合,則點![]() 與數 表示的點重合;
與數 表示的點重合;
(3)點![]() 、
、![]() 、
、![]() 開始在數軸上運動,若點
開始在數軸上運動,若點![]() 以每秒1個單位長度的速度向左運動,同時,點
以每秒1個單位長度的速度向左運動,同時,點![]() 和點
和點![]() 分別以每秒2個單位長度和4個單位長度的速度向右運動,假設
分別以每秒2個單位長度和4個單位長度的速度向右運動,假設![]() 秒鐘過后,若點
秒鐘過后,若點![]() 與點
與點![]() 之間的距離表示為
之間的距離表示為![]() ,點
,點![]() 與點
與點![]() 之間的距離表示為
之間的距離表示為![]() ,點
,點![]() 與點
與點![]() 之間的距離表示為
之間的距離表示為![]() ,求
,求![]() 、
、![]() 、
、![]() 的長(用含
的長(用含![]() 的式子表示);
的式子表示);
(4)在(3)的條件下,![]() 的值是否隨著時間
的值是否隨著時間![]() 的變化而改變?若改變,請說明理由;若不變,請求其值.
的變化而改變?若改變,請說明理由;若不變,請求其值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀材料:我們知道:點A.B在數軸上分別表示有理數a、b,A.B兩點之間的距離表示為AB,在數軸上A.B兩點之間的距離AB=|a-b|.所以式子|x3|的幾何意義是數軸上表示有理數3的點與表示有理數x的點之間的距離.
根據上述材料,解答下列問題:
![]()
(1)若|x3|=4,則x=______;
(2)式子|x3|=|x+1|,則x=______;
(3)若|x3|+|x+1|=9,借助數軸求x的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下面是某街區的平面示意圖,根據要求答題.

(1)這幅圖的比例尺是( )
(2)學校位于廣場的( )面(填東、南、西、北)( )千米處.
(3)人民公園位于廣場的東偏南![]() 方向3千米處.在圖中標出它的位置.
方向3千米處.在圖中標出它的位置.
(4)廣場的西面1千米處,有一條商業街與人民路垂直,在圖中畫線表示商業街.
查看答案和解析>>
科目:初中數學 來源: 題型:
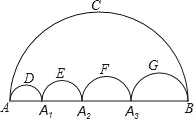
【題目】圖中的五個半圓,鄰近的兩半圓相切,兩只小蟲同時出發,以相同的速度從A點到B點,甲蟲沿ADA1、A1EA2、A2FA3、A3GB路線爬行,乙蟲沿ACB路線爬行,則下列結論正確的是( )
A. 甲先到B點 B. 乙先到B點 C. 甲、乙同時到B D. 無法確定
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】點D、E分別是△ABC兩邊AB、BC所在直線上的點,∠BDE+∠ACB=180°,DE=AC,AD=2BD.


(1) 如圖1,當點D、E分別在AB、CB的延長線上時,求證:BE=BD
(2) 如圖2,當點D、E分別在AB、BC邊上時,BE與BD存在怎樣的數量關系?請寫出你的結論,并證明
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com