
【題目】如圖,一次函數y=ax+b的圖像與正比例函數y=kx的圖像交于點M,
(1)求正比例函數和一次函數的解析式;
(2)根據圖像寫出使正比例函數的值大于一次函數的值的x的取值范圍;
(3)求ΔMOP的面積。
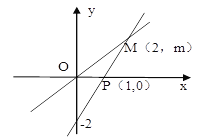
【答案】(1)一次函數表達式為: y=2x-2;正比例函數為 y=x;(2)x<2;(3)1.
【解析】∵y=ax+b經過(1,0)和(0,-2)
∴![]() …………………………………………………1分
…………………………………………………1分
解得:k=2 b=-2…………………………………………..2分
一次函數表達式為: y=2x-2…………………………………3分
∵點M在該一次函數上,∴m=2 x 2-2=2
M點坐標為(2,2)……………………………………………4分
又∵M在函數 y=kx上,∴ k=m/2=2/2=1
∴正比例函數為 y=x…………………………………………..5分
(2)由圖像可知,當x=2時,一次函數與正比例函數相交;x<2時,正比例函數圖像在一次函數上方,故:
x<2時,x>2x-2………………………………………………….7分
(3)作MN垂直X軸,易知MN=2
∴故SΔMOP=1/2 x 1 x 2=1


科目:初中數學 來源: 題型:
【題目】某中學八年級組織了一次“漢字聽寫比賽”,每班選25名同學參加比賽,成績分為A,B,C,D四個等級,其中A等級得分為100分,B等級得分為85分,C等級得分為75分,D等級得分為60分,語文教研組將八年級一班和二班的成績整理并繪制成如下的統計圖,請根損換供的信息解答下列問題.
(1)把一班比賽成統計圖補充完整;

(2)填表:
平均數(分) | 中位數(分) | 眾數(分) | |
一班 | a | b | 85 |
二班 | 84 | 75 | c |
表格中:a=______,b=______,c=_______.
(3)請從以下給出的兩個方面對這次比賽成績的結果進行分析:
①從平均數、眾數方面來比較一班和二班的成績;
②從B級以上(包括B級)的人數方面來比較-班和二班的成績.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】給出如下定義:如果兩個不相等的有理數a,b滿足等式a-b=ab.那么稱a,b是“關聯有理數對”,記作(a,b).如:因為![]() ,
,![]() .所以數對(3,
.所以數對(3,![]() )是“關聯有理數對”.
)是“關聯有理數對”.
(1)在數對①(1,![]() )、②(-1,0)、③(
)、②(-1,0)、③(![]() ,
,![]() )中,是“關聯有理數對”的是____________(只填序號);
)中,是“關聯有理數對”的是____________(只填序號);
(2)若(m,n)是“關聯有理數對”,則(-m,-n)___________“關聯有理數對”(填“是”或“不是”);
(3)如果兩個有理數是一對“關聯有理數對”,其中一個有理數是5,求另一個有理數.
查看答案和解析>>
科目:初中數學 來源: 題型:
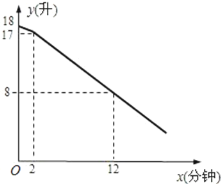
【題目】教室里放有一臺飲水機(如圖),飲水機上有兩個放水管.課間同學們依次到飲水機前用茶杯接水.假設接水過程中水不發生潑灑,每個同學所接的水量都是相等的.兩個放水管同時打開時,它們的流量相同.放水時先打開一個水管,過一會兒,再打開第二個水管,放水過程中閥門一直開著.飲水機的存水量y(升)與放水時間x(分鐘)的函數關系如圖所示:
(1)求出飲水機的存水量y(升)與放水時間x(分鐘)(x≥2)的函數關系式;
(2)如果打開第一個水管后,2分鐘時恰好有4個同學接水結束,則前22個同學接水結束共需要幾分鐘?
(3)按(2)的放法,求出在課間10分鐘內班級中最多有多少個同學能及時接完水?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“低碳生活,綠色出行”,自行車正逐漸成為人們喜愛的交通工具.某運動商城的自行車銷售量自2017年起逐月增加,據統計,該商城1月份銷售自行車64輛,3月份銷售了100輛.
(1)若該商城前4個月的自行車銷量的月平均增長率相同,問該商城4月份賣出多少輛自行車?
(2)考慮到自行車需求不斷增加,該商城準備投入3萬元再購進一批兩種規格的自行車,已知A型車的進價為500元/輛,售價為700元/輛,B型車進價為1000元/輛,售價為1300元/輛.根據銷售經驗,A型車不少于B型車的2倍,但不超過B型車的2.8倍.假設所進車輛全部售完,為使利潤最大,該商城應如何進貨?
查看答案和解析>>
科目:初中數學 來源: 題型:
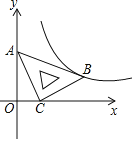
【題目】在平面直角坐標系![]() 中,將一塊含有45°角的直角三角板如圖放置,直角頂點C的坐標(1,0),頂點A的坐標為(0, 2),頂點B恰好落在第一象限的雙曲線上,現將直角三角板沿x軸正方向平移,當頂點A恰好落在該雙曲線上時停止運動,則此時點C的對應點
中,將一塊含有45°角的直角三角板如圖放置,直角頂點C的坐標(1,0),頂點A的坐標為(0, 2),頂點B恰好落在第一象限的雙曲線上,現將直角三角板沿x軸正方向平移,當頂點A恰好落在該雙曲線上時停止運動,則此時點C的對應點![]() 的坐標為__________
的坐標為__________
查看答案和解析>>
科目:初中數學 來源: 題型:
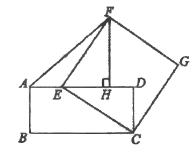
【題目】如圖,在矩形ABCD中,AD=4,點E在邊AD上,連接CE,以CE為邊向右上方作正方形CEFG,作FH⊥AD,垂足為H,連接AF.
(1)求證:FH=ED;
(2)當AE為何值時,△AEF的面積最大?
查看答案和解析>>
科目:初中數學 來源: 題型:
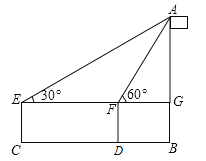
【題目】如圖,小麗準備測一根旗桿AB的高度,已知小麗的眼睛離地面的距離EC=1.5米,第一次測量點C和第二次測量點D之間的距離CD=10米,∠AEG=30°,∠AFG=60°,請你幫小麗計算出這根旗桿的高度.(結果保留根號)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com