Question

【題目】某中學計劃從辦公用品公司購買A，B兩種型號的小黑板．經洽談，購買一塊A型小黑板比購買一塊B型小黑板多用20元，且購買5塊A型小黑板和4塊B型小黑板共需820元．
（1）求購買一塊A型小黑板、一塊B型小黑板各需多少元．
（2）根據該中學實際情況，需從公司購買A，B兩種型號的小黑板共60塊，要求購買A，B兩種型號小黑板的總費用不超過5240元．并且購買A型小黑板的數量不小于購買B型小黑板數量的 ．則該中學從公司購買A，B兩種型號的小黑板有哪幾種方案？哪種方案的總費用最低？

Answer 1

【答案】
（1）解：設一塊A型小黑板x元，一塊B型小黑板y元．

則 ，

解得 ．

答：一塊A型小黑板100元，一塊B型小黑板80元

（2）解：設購買A型小黑板m塊，則購買B型小黑板（60﹣m）塊

則 ，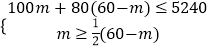

解得20≤m≤22，

又∵m為正整數

∴m=20，21，22

則相應的60﹣m=40，39，38

∴共有三種購買方案，分別是

方案一：購買A型小黑板20塊，購買B型小黑板40塊；

方案二：購買A型小黑板21塊，購買B型小黑板39塊；

方案三：購買A型小黑板22塊，購買B型小黑板38塊．

方案一費用為100×20+80×40=5200元；

方案二費用為100×21+80×39=5220元；

方案三費用為100×22+80×38=5240元．

∴方案一的總費用最低，

即購買A型小黑板20塊，購買B型小黑板40塊總費用最低，為5200元

【解析】（1）設購買一塊A型小黑板需要x元，一塊B型為y元，根據等量關系：購買一塊A型小黑板比買一塊B型小黑板多用20元；購買5塊A型小黑板和4塊B型小黑板共需820元；可列方程組求解．（2）設購買A型小黑板m塊，則購買B型小黑板（60﹣m）塊，根據需從公司購買A、B兩種型號的小黑板共60塊，要求購買A、B兩種型號小黑板的總費用不超過5240元．并且購買A型小黑板的數量不小于購買B型小黑板數量的 ，可列不等式組求解．
【考點精析】關于本題考查的一元一次不等式組的應用，需要了解1、審：分析題意，找出不等關系；2、設：設未知數；3、列：列出不等式組；4、解：解不等式組；5、檢驗：從不等式組的解集中找出符合題意的答案；6、答：寫出問題答案才能得出正確答案．