
【題目】如圖,把 ![]() 個邊長為1的正方形拼接成一排,求得
個邊長為1的正方形拼接成一排,求得 ![]() ,
, ![]() ,
, ![]() ,計算
,計算 ![]() , ……按此規律,寫出
, ……按此規律,寫出 ![]() (用含
(用含 ![]() 的代數式表示).
的代數式表示).
【答案】![]()
![]() ;
;![]()
【解析】解:如圖,過點C作CE⊥A4B于E,易得∠A4BC=∠BA4A1 ,
故tan∠A4BC=tan∠BA4A1=![]() ,
,
在Rt△BCE中,由tan∠A4BC=![]() ,得BE=4CE,而BC=1,
,得BE=4CE,而BC=1,
則BE=![]() , CE=
, CE=![]() ,
,
而A4B=![]() ,
,
所以A4E=A4B-BE=![]() ,
,
在Rt△A4EC中,tan∠BA4C=![]() 。
。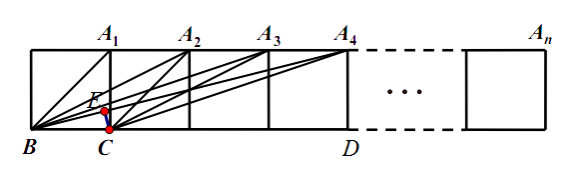
根據前面的規律,不能得出tan∠ BA1C=![]() ,tan∠ BA2C=
,tan∠ BA2C=![]() ,tan∠ BA3C=
,tan∠ BA3C=![]() ,tan∠ BA4C=
,tan∠ BA4C=![]()
則可得規律tan∠ BAnC=![]() =
=![]() 。
。
所以答案是![]() ;
;![]()
【考點精析】根據題目的已知條件,利用解直角三角形的相關知識可以得到問題的答案,需要掌握解直角三角形的依據:①邊的關系a2+b2=c2;②角的關系:A+B=90°;③邊角關系:三角函數的定義.(注意:盡量避免使用中間數據和除法).


科目:初中數學 來源: 題型:
【題目】如圖,將Rt△ABC(其中∠B=35°,∠C=90°)繞點A按順時針方向旋轉到△AB1C1的位置,使得點C、A、B1在同一條直線上,那么旋轉角的度數是 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了能以“更新、更綠、更潔、更寧”的城市形象迎接2011年大運會的召開,深圳市全面實施市容市貌環境提升行動,某工程隊承擔了一段長1500米的道路綠化工程,施工時有兩種綠化方案:
甲方案是綠化1米的道路需要A型花2枝和B型花3枝,成本是22元;
乙方案是綠化1米的道路需要A型花1枝和B型花5枝,成本是25元.
現要求按照乙方案綠化道路的總長度不能少于按甲方案綠化道路的總長度的2倍.
(1)求A型花和B型花每枝的成本分別是多少元?
(2)求當按甲方案綠化的道路總長度為多少米時,所需工程的總成本最少?總成本最少是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小張在甲樓A處向外看,由于受到前面乙樓的遮擋,最近只能看到地面D處,俯角為α.小穎在甲樓B處(B在A的正下方)向外看,最近能看到地面E處,俯角為β,地面上G,F,D,E在同一直線上,已知乙樓高CF為10m,甲乙兩樓相距FG為15m,俯角α=45°,β=35°.
(1)求點A到地面的距離AG;
(2)求A,B之間的距離.(結果精確到0.1m)(sin35°≈0.57,cos35°≈0.82,tan35°≈0.70)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知△ABC,AB=AC,若以點B為圓心,BC長為半徑畫弧,交腰AC于點E,則下列結論一定正確的是( )
A.AE=EC
B.AE=BE
C.∠EBC=∠BAC
D.∠EBC=∠ABE
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知△ABC,AB=AC,D為直線BC上一點,E為直線AC上一點,AD=AE,設∠BAD=α,∠CDE=β.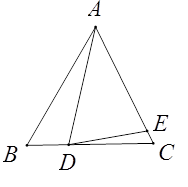
(1)如圖,若點D在線段BC上,點E在線段AC上.
①如果∠ABC=60°,∠ADE=70°,那么α=°,β=°.②求α,β之間的關系式.
(2)是否存在不同于以上②中的α,β之間的關系式?若存在,請求出這個關系式(求出一個即可);若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,以△ABC的BC邊上一點O為圓心,經過A,C兩點且與BC邊交于點E,點D為CE的下半圓弧的中點,連接AD交線段EO于點F,若AB=BF. 
(1)求證:AB是⊙O的切線;
(2)若CF=4,DF= ![]() ,求⊙O的半徑r及sinB.
,求⊙O的半徑r及sinB.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com