
【題目】如圖,拋物線 ![]() 的圖象與x軸交于A(﹣1.0),B(3,0)兩點,與y軸交于點C(0,﹣3),頂點為D.
的圖象與x軸交于A(﹣1.0),B(3,0)兩點,與y軸交于點C(0,﹣3),頂點為D.
(1)求此拋物線的解析式.
(2)求此拋物線頂點D的坐標和對稱軸.
(3)探究對稱軸上是否存在一點P,使得以點P、D、A為頂點的三角形是等腰三角形?若存在,請求出所有符合條件的P點的坐標,若不存在,請說明理由.
【答案】
(1)解:∵拋物線 ![]() 的圖象與x軸交于A(﹣1.0),B(3,0)兩點,與y軸交于點C(0,﹣3),
的圖象與x軸交于A(﹣1.0),B(3,0)兩點,與y軸交于點C(0,﹣3),
∴  ,
,
解得:  ,
,
∴拋物線的解析式是 ![]()
(2)解:∵ ![]() =
= ![]() ,
,
∴此拋物線頂點D的坐標是(1,﹣4),對稱軸是直線x=1
(3)解:存在一點P,使得以點P、D、A為頂點的三角形是等腰三角形,設(shè)點P的坐標為(1,y),分三種情況討論:
①當PA=PD時 ![]() =
= ![]() ,
,
解得,y= ![]() ,
,
即點P的坐標為(1, ![]() );
);
②當DA=DP時, ![]() =
= ![]() ,
,
解得,y= ![]() ,
,
即點P的坐標為(1, ![]() )或(1,
)或(1, ![]() );
);
③當AD=AP時, ![]() =
= ![]() ,
,
解得,y=±4,
即點P的坐標是(1,4)或(1,﹣4),當點P為(1,﹣4)時與點D重合,故不符合題意.
由上可得,以點P、D、A為頂點的三角形是等腰三角形時,點P的坐標為(1, ![]() )或(1,
)或(1, ![]() )或(1,
)或(1, ![]() )或(1,4).
)或(1,4).
【解析】(1)根據(jù)題意得一個三元一次方程組,解之即可得拋物線解析式.
(2)根據(jù)(1)中得出的解析式,配成頂點式,從而得出頂點式和對稱軸.
(3)存在一點P,使得以點P、D、A為頂點的三角形是等腰三角形,設(shè)點P的坐標為(1,y),分三種情況討論:①當PA=PD時,②當DA=DP時,③當AD=AP時,根據(jù)兩點間距離公式計算即可得出P點坐標.


科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,鉛球運動員擲鉛球的高度y(m)與水平距離x(m)之間的函數(shù)關(guān)系式是y=﹣ ![]() x2+
x2+ ![]() x+
x+ ![]() ,則該運動員此次擲鉛球的成績是( )
,則該運動員此次擲鉛球的成績是( )
A.6m
B.12m
C.8m
D.10m
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】為確保信息安全,在傳輸時往往需加密,發(fā)送方發(fā)出一組密碼a,b,c時,則接收方對應(yīng)收到的密碼為A,B,C.雙方約定:A=2a﹣b,B=2b,C=b+c,例如發(fā)出1,2,3,則收到0,4,5.
(1)當發(fā)送方發(fā)出一組密碼為2,3,5時,則接收方收到的密碼是多少?
(2)當接收方收到一組密碼2,8,11時,則發(fā)送方發(fā)出的密碼是多少?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某單位認真開展學(xué)習(xí)和實踐科學(xué)發(fā)展觀活動,在階段總結(jié)中提出對本單位今后的整改措施,并在征求職工對整改方案的滿意程度時進行民主測評,測評等級為:很滿意、較滿意、滿意、不滿意四個等級.

(1)若測評后結(jié)果如扇形圖(圖①),且測試等級為很滿意、較滿意、滿意、不滿意的人數(shù)之比為2:5:4:1,則圖中a= ° ,β= °.
(2)若測試后部分統(tǒng)計結(jié)果如直方圖(圖②),請將直方圖補畫完整,并求出該單位職工總?cè)藬?shù)為 人.
(3)按上級要求,滿意度必須不少于95%方案才能通過,否則,必須對方案進行完善.若要使該方案完善后能獲得通過,至少還需增加 人對該方案的測評等級達滿意(含滿意)以上.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖![]() ,在平面直角坐標系中,點
,在平面直角坐標系中,點![]() ,
,![]() 的坐標分別為
的坐標分別為![]() ,
,![]() ,將線段
,將線段![]() 先向上平移
先向上平移![]() 個單位長度,再向右平移
個單位長度,再向右平移![]() 個單位長度,得到線段
個單位長度,得到線段![]() ,連接
,連接![]() ,
,![]() ,構(gòu)成平行四邊形
,構(gòu)成平行四邊形![]() .
.
(1)請寫出點![]() 的坐標為________,點
的坐標為________,點![]() 的坐標為________,
的坐標為________,![]() ________;
________;
(2)點![]() 在
在![]() 軸上,且
軸上,且![]() ,求出點
,求出點![]() 的坐標;
的坐標;
(3)如圖![]() ,點
,點![]() 是線段
是線段![]() 上任意一個點(不與
上任意一個點(不與![]() 、
、![]() 重合),連接
重合),連接![]() 、
、![]() ,試探索
,試探索![]() 、
、![]() 、
、![]() 之間的關(guān)系,并證明你的結(jié)論.
之間的關(guān)系,并證明你的結(jié)論.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖6,已知箭頭的方向是水流的方向,一艘游艇從江心島的右側(cè)A點逆流航行3小時到達B點后,又繼續(xù)順流航行2.5小時后到達C點,總共航行了208千米,已知水流的速度是2千米/時。
(1)求游艇在靜水中的速度。
(2)由于AC段在建橋,游艇用同樣的速度沿原路返回共需多少時間?(結(jié)果保留一位小數(shù))
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
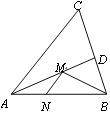
【題目】如圖,在銳角△ABC中,AB=4,∠BAC=45°,∠BAC的平分線交BC于點D,M、N分別是AD和AB上的動點,則BM+MN的最小值是__________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,∠B、∠D的兩邊分別平行.
(1)在圖1中, ∠B與∠D的數(shù)量關(guān)系是 ;
(2)在圖2中, ∠B與∠D的數(shù)量關(guān)系是 ;
(3)用一句話歸納的結(jié)論為
(4)應(yīng)用:若兩個角的兩邊分別互相平行,其中一個角比另一個角的2倍小30°,求著兩個角的度數(shù).

查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com