
【題目】如圖,在矩形ABCD中,AD=2AB,點M、N分別在邊AD、BC上,連接BM、DN.若四邊形MBND是菱形,則 ![]() 等于( )
等于( ) 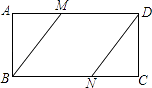
A.![]()
B.![]()
C.![]()
D.![]()
【答案】C
【解析】解:∵四邊形MBND是菱形,
∴MD=MB.
∵四邊形ABCD是矩形,
∴∠A=90°.
設AB=x,AM=y,則MB=2x﹣y,(x、y均為正數).
在Rt△ABM中,AB2+AM2=BM2 , 即x2+y2=(2x﹣y)2 ,
解得x= ![]() y,
y,
∴MD=MB=2x﹣y= ![]() y,
y,
∴ ![]() =
= ![]() =
= ![]() .
.
故選:C.
【考點精析】掌握勾股定理的概念和菱形的性質是解答本題的根本,需要知道直角三角形兩直角邊a、b的平方和等于斜邊c的平方,即;a2+b2=c2;菱形的四條邊都相等;菱形的對角線互相垂直,并且每一條對角線平分一組對角;菱形被兩條對角線分成四個全等的直角三角形;菱形的面積等于兩條對角線長的積的一半.


科目:初中數學 來源: 題型:
【題目】通過平移得到的圖形中的每一個點與原圖形中的對應點所連線段( )
A. 平行 B. 在同一條直線上
C. 相等 D. 平行(或在同一條直線上)且相等
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于一組數據3,3,2,3,6,3,10,3,6,3,2:①眾數是3;②眾數與中位數的數值不等;③中位數與平均數的數值相等;④平均數與眾數的數值相等,其中正確的結論有( )
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,把點P(﹣2,1)繞原點O順時針旋轉180°,所得到的對應點P′的坐標為( )
A.(2,﹣1)
B.(﹣2,1)
C.(2,1)
D.(﹣2,﹣1)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com