
【題目】為了貫徹落實國務院關于促進家電下鄉的指示精神,有關部門自2007年12月底起進行了家電下鄉試點,對彩電、冰箱(含冰柜)、手機三大類產品給予產品銷售價格13%的財政資金直補.企業數據顯示,截至2008年12月底,試點產品已銷售350萬臺(部),銷售額達50億元,與上年同期相比,試點產品家電銷售量增長了40%.
(1)求2007年同期試點產品類家電銷售量為多少萬臺(部)?
(2)如果銷售家電的平均價格為:彩電每臺1500元,冰箱每臺2000元,手機每部800元,已知銷售的冰箱(含冰柜)數量是彩電數量的![]() 倍,求彩電、冰箱、手機三大類產品分別銷售多少萬臺(部),并計算獲得的政府補貼分別為多少萬元?
倍,求彩電、冰箱、手機三大類產品分別銷售多少萬臺(部),并計算獲得的政府補貼分別為多少萬元?
【答案】(1)2007年同期試點產品類家電銷售量為250萬臺(部);(2)彩電、冰箱、手機三大類產品分別銷售88萬臺、132萬臺、130萬部,獲得的政府補貼分別為17160萬元、34320萬元、13520萬元.
【解析】
試題分析:(1)本題中“截至2008年12月底,”“與上年同期相比,試點產品家電銷售量增長了40%”,所以可先設07年的銷售量,然后表示出08年的銷售量,再根據“截至2008年12月底,試點產品已銷售350萬臺(部)”,即可列出方程;
(2)要把握好兩個關鍵語:“已知銷售的冰箱(含冰柜)數量是彩電數量的![]() 倍,”“銷售額達50億”,然后根據彩電的銷售額+冰箱的銷售額+手機的銷售額=總銷售額.列出方程求解.
倍,”“銷售額達50億”,然后根據彩電的銷售額+冰箱的銷售額+手機的銷售額=總銷售額.列出方程求解.
解:(1)設2007年銷量為a萬臺,則a(1+40%)=350,
解之得:a=250;
答:2007年同期試點產品類家電銷售量為250萬臺(部);
(2)設銷售彩電x萬臺,則銷售冰箱![]() x萬臺,銷售手機(350﹣
x萬臺,銷售手機(350﹣![]() x)萬臺.
x)萬臺.
由題意得:1500x+2000×![]() x+800(350﹣
x+800(350﹣![]() x)=500000.
x)=500000.
解得:x=88.
∴![]() x=132,350﹣
x=132,350﹣![]() x=130.
x=130.
所以,彩電、冰箱(含冰柜)、手機三大類產品分別銷售88萬臺、132萬臺、130萬部.
∴88×1500×13%=17160(萬元),132×2000×13%=34320(萬元),
130×800×13%=13520(萬元).
獲得的政府補貼分別是17160萬元、34320萬元、13520萬元.
答:彩電、冰箱、手機三大類產品分別銷售88萬臺、132萬臺、130萬部,獲得的政府補貼分別為17160萬元、34320萬元、13520萬元.


 輕松暑假總復習系列答案
輕松暑假總復習系列答案科目:初中數學 來源: 題型:
【題目】如圖,方格紙中的每個小方格都是邊長為1個單位的正方形,在建立平面直角坐標系后,△ABC的頂點均在格點上,點C的坐標為(4,﹣1).
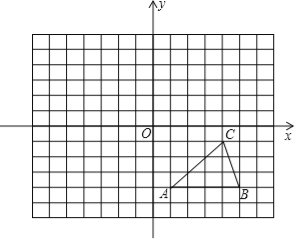
(1)把△ABC向上平移5個單位后得到對應的△A1B1C1,畫出△A1B1C1,并寫出C1的坐標;
(2)以原點O為對稱中心,再畫出與△A1B1C1關于原點O對稱的△A2B2C2,并寫出點C2的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】計算
(1)x(﹣x2)x3;
(2)(xy)5÷(xy)3
(3)a5(﹣a)3+(﹣2a2)4;
(4)|﹣2|+(﹣2)2+(7﹣π)0﹣(![]() )﹣1.
)﹣1.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在如圖所示的方格紙上,只用直尺畫圖.

(1)過點P作直線CD∥AB.
(2)作EB⊥AB,交直線CD于E點.
(3)過點P作出點P到直線AB的垂線段PQ,垂足為點Q,并量出點P到直線AB的距離(精確到0.1cm).
(4)比較線段BE與線段PQ的大小.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】到一個三角形三個頂點的距離都相等的點是這個三角形的( )
A. 三條中線的交點 B. 三條角平分線的交點
C. 三條高的交點 D. 三條邊的垂直平分線的交點
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】根據下列條件,能判定一個三角形是直角三角形的是( )
A.三條邊的邊長之比是1:2:3
B.三個內角的度數之比是1:1:2
C.三條邊的邊長分別是![]() ,
,![]() ,
,![]()
D.三條邊的邊長分別是12,15,20
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】所謂配方,就是把一個多項式經過適當變形配成完全平方式.配方法除一元二次方程求根公式推導這一典型應用外,在因式分解、化簡二次根式、證明恒等式、解方程、求代數式最值等問題中都有廣泛應用.是一種很重要、很基本的數學方法.如以下例1,例2:
例1:分解因式 x2﹣120x+3456
解:原式=x2﹣120x+3600+3456﹣3600
=(x﹣60)2﹣144
=(x﹣60+12)(x﹣60﹣12)
=(x﹣48)(x﹣72)
例2:化簡:![]()
解:原式=![]()
=![]()
=![]() ﹣
﹣![]()
閱讀以上材料,請問答以下問題:
(1)分解因式:x2﹣40x+319= ;
(2)化簡:![]() ;
;
(3)利用配方法求4x2+y2﹣2y﹣4x+15的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com