
【題目】如圖,矩形ABCD中,AB=8,點E是AD上的一點,有AE=4,BE的垂直平分線交BC的延長線于點F,連結(jié)EF交CD于點G.若G是CD的中點,則BC的長是 . 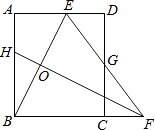
【答案】7
【解析】解:∵矩形ABCD中,G是CD的中點,AB=8, ∴CG=DG= ![]() ×8=4,
×8=4,
在△DEG和△CFG中,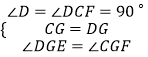 ,
,
∴△DEG≌△CFG(ASA),
∴DE=CF,EG=FG,
設(shè)DE=x,
則BF=BC+CF=AD+CF=4+x+x=4+2x,
在Rt△DEG中,EG= ![]() =
= ![]() ,
,
∴EF=2 ![]() ,
,
∵FH垂直平分BE,
∴BF=EF,
∴4+2x=2 ![]() ,
,
解得x=3,
∴AD=AE+DE=4+3=7,
∴BC=AD=7.
故答案為:7.
根據(jù)線段中點的定義可得CG=DG,然后利用“角邊角”證明△DEG和△CFG全等,根據(jù)全等三角形對應(yīng)邊相等可得DE=CF,EG=FG,設(shè)DE=x,表示出BF,再利用勾股定理列式求EG,然后表示出EF,再根據(jù)線段垂直平分線上的點到兩端點的距離相等可得BF=EF,然后列出方程求出x的值,從而求出AD,再根據(jù)矩形的對邊相等可得BC=AD.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,反比例函數(shù)y= ![]() (x>0)的圖象經(jīng)過矩形OABC對角線的交點M,分別與AB、BC相交于點D、E.,則下列結(jié)論正確的是(將正確的結(jié)論填在橫線上).
(x>0)的圖象經(jīng)過矩形OABC對角線的交點M,分別與AB、BC相交于點D、E.,則下列結(jié)論正確的是(將正確的結(jié)論填在橫線上).
①s△OEB=s△ODB , ②BD=4AD,③連接MD,S△ODM=2S△OCE , ④連接ED,則△BED∽△BCA.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知,如圖,點A、D、B、E在同一直線上,AC=EF,AD=BE,∠A=∠E,
(1)求證:△ABC≌△EDF;
(2)當(dāng)∠CHD=120°,猜想△HDB的形狀,并說明理由.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】根據(jù)2008~2012年杭州市實現(xiàn)地區(qū)生產(chǎn)總值(簡稱GDP,單位:億元)統(tǒng)計圖所提供的信息,下列判斷正確的是( ) 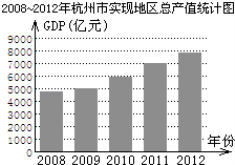
A.2010~2012年杭州市每年GDP增長率相同
B.2012年杭州市的GDP比2008年翻一番
C.2010年杭州市的GDP未達(dá)到5500億元
D.2008~2012年杭州市的GDP逐年增長
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】四邊形ABCD是直角梯形,AB∥CD,AB⊥BC,且BC=CD=2,AB=3,把梯形ABCD分別繞直線AB,CD旋轉(zhuǎn)一周,所得幾何體的表面積分別為S1 , S2 , 則|S1﹣S2|=(平方單位) 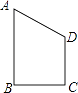
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知正方形ABCD的邊長為4,對稱中心為點P,點F為BC邊上一個動點,點E在AB邊上,且滿足條件∠EPF=45°,圖中兩塊陰影部分圖形關(guān)于直線AC成軸對稱,設(shè)它們的面積和為S1 . 
(1)求證:∠APE=∠CFP;
(2)設(shè)四邊形CMPF的面積為S2 , CF=x, ![]() .
.
①求y關(guān)于x的函數(shù)解析式和自變量x的取值范圍,并求出y的最大值;
②當(dāng)圖中兩塊陰影部分圖形關(guān)于點P成中心對稱時,求y的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
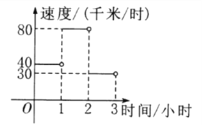
【題目】某人駕車從鄉(xiāng)村進(jìn)城.各時間段的行駛速度如圖所示.當(dāng)![]() 時,其行駛路程
時,其行駛路程![]() 與時間
與時間![]() 之間的函數(shù)表達(dá)式是________,當(dāng)
之間的函數(shù)表達(dá)式是________,當(dāng)![]() 時,其行駛路程
時,其行駛路程![]() 與時間
與時間![]() 之間的函數(shù)表達(dá)式是________,當(dāng)
之間的函數(shù)表達(dá)式是________,當(dāng)![]() 時,其行駛路程
時,其行駛路程![]() 與時間
與時間![]() 之間的函數(shù)表達(dá)式是________.
之間的函數(shù)表達(dá)式是________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】定義符號min{a,b}的含義為:當(dāng)a≥b時min{a,b}=b;當(dāng)a<b時min{a,b}=a.如:min{1,﹣3}=﹣3,min{﹣4,﹣2}=﹣4.則min{﹣x2+1,﹣x}的最大值是( )
A.![]()
B.![]()
C.1
D.0
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】閱讀材料并解答下列問題.
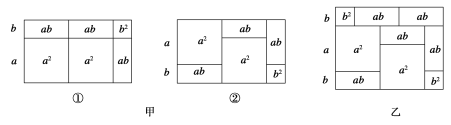
你知道嗎?一些代數(shù)恒等式可以用平面圖形的面積來表示,例如(2a+b)(a+b)=2a2+3ab+b2就可以用圖甲中的①或②的面積表示.
(1)請寫出圖乙所表示的代數(shù)恒等式;
(2)畫出一個幾何圖形,使它的面積能表示(a+b)(a+3b)=a2+4ab+3b2;
(3)請仿照上述式子另寫一個含有a,b的代數(shù)恒等式,并畫出與之對應(yīng)的幾何圖形.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com