
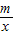 ,利用待定系數法求反比例函數解析式解答即可;
,利用待定系數法求反比例函數解析式解答即可;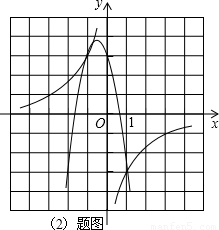 解:(1)當k=-3時,A(1,-3),
解:(1)當k=-3時,A(1,-3),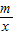 ,
,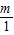 =-3,
=-3,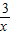 ;
; )2-
)2- k的對稱軸為:直線x=-
k的對稱軸為:直線x=- ,
, 時,才能使得y隨著x的增大而增小,
時,才能使得y隨著x的增大而增小, .
.

科目:初中數學 來源: 題型:
 在平面直角坐標系內,已知點A(2,1),O為坐標原點.請你在坐標軸上確定點P,使得△AOP成為等腰三角形.在給出的坐標系中把所有這樣的點P都找出來,畫上實心點,并在旁邊標上P1,P2,…,PK的坐標(有k個就標到PK為止,不必寫出畫法).
在平面直角坐標系內,已知點A(2,1),O為坐標原點.請你在坐標軸上確定點P,使得△AOP成為等腰三角形.在給出的坐標系中把所有這樣的點P都找出來,畫上實心點,并在旁邊標上P1,P2,…,PK的坐標(有k個就標到PK為止,不必寫出畫法).查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com