
【題目】如圖,在菱形ABCD中,∠A=110°,E , F分別是邊AB和BC的中點,EP⊥CD于點P , 求∠FPC . 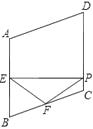
【答案】解答:解:延長PF交AB的延長線于點G , ,在△BGF與△CPF中, 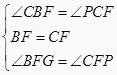 ,∴△BGF≌△CPF , ∴GF=PF , ∴F為PG中點.又∵EP⊥CD , ∴∠BEP=90°,∴EF=
,∴△BGF≌△CPF , ∴GF=PF , ∴F為PG中點.又∵EP⊥CD , ∴∠BEP=90°,∴EF= ![]() PG ,
PG ,
∵PF= ![]() PG(中點定義),∴EF=PF , ∴∠FEP=∠EPF , ∵∠BEP=∠EPC=90°,∴∠BEP-∠FEP=∠EPC-∠EPF , 即∠BEF=∠FPC , ∵四邊形ABCD為菱形,∴AB=BC , ∠ABC=180°-∠A=70°,∵E , F分別為AB , BC的中點,∴BE=BF , ∠BEF=∠BFE=
PG(中點定義),∴EF=PF , ∴∠FEP=∠EPF , ∵∠BEP=∠EPC=90°,∴∠BEP-∠FEP=∠EPC-∠EPF , 即∠BEF=∠FPC , ∵四邊形ABCD為菱形,∴AB=BC , ∠ABC=180°-∠A=70°,∵E , F分別為AB , BC的中點,∴BE=BF , ∠BEF=∠BFE= ![]() (180°-70°)=55°,∴∠FPC=55°.
(180°-70°)=55°,∴∠FPC=55°.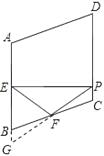
【解析】延長PF交AB的延長線于點G . 根據已知可得∠ABC , ∠BEF , ∠BFE的度數,再根據余角的性質可得到∠EPF的度數,從而不難求得∠FPC的度數.
【考點精析】關于本題考查的勾股定理的概念和菱形的性質,需要了解直角三角形兩直角邊a、b的平方和等于斜邊c的平方,即;a2+b2=c2;菱形的四條邊都相等;菱形的對角線互相垂直,并且每一條對角線平分一組對角;菱形被兩條對角線分成四個全等的直角三角形;菱形的面積等于兩條對角線長的積的一半才能得出正確答案.


科目:初中數學 來源: 題型:
【題目】2015年初,一列CRH5型高速車組進行了“300000公里正線運營考核”標志著中國高速快車從“中國制造”到“中國創造”的飛躍,將300000用科學記數法表示為( )
A.3×106
B.3×105
C.0.3×106
D.30×104
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知∠ABC是平角,過點B任意作一條射線BD,將∠ABC分成∠DBA與∠DBC兩個角.
(1)當∠DBA是什么角時,∠DBA>∠DBC?
(2)當∠DBA是什么角時,∠DBA=∠DBC?
(3)當∠DBA是什么角時,∠DBA<∠DBC?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】世界文化遺產長城總長約為6700000m,若將6700000用科學記數法表示為6.7×10n(n是正整數),則n的值為( )
A.5
B.6
C.7
D.8
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學生為調查本校學生平均每天完成作業所用時間的情況,隨機調查了50名同學,下圖是根據調查所得數據繪制的統計圖的一部分.
請根據以上信息,解答下列問題:
(1)將統計圖補充完整;
(2)若該校共有1800名學生,根據以上調查結果估計該校全體學生每天完成作業所用總時間.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某單位面向內部職工招聘高級管理人員一名.經初選、復選后,共有甲、乙、丙三名候選人進入最后的決賽.現對甲、乙、丙三人進行了筆試和面試兩項測試,三人的測試成績如下表所示: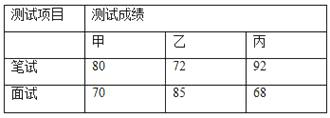
除了筆試、面試外,根據錄用程序,該單位還組織了200名職工利用投票推薦的方式對三人進行民主評議,三人的得票率如下圖所示(沒有棄權票,每位職工只能推薦1人),每得一票記1分.
(1)甲的民主評議得分為多少?
(2)若根據筆試成績、面試成績、民主評議得分三項的平均成績確定個人成績,那么誰將被錄用?
(3)根據實際需要,該單位將筆試、面試、民主評議三項得分按5:3:2的比例確定個人成績,那么誰將被錄用?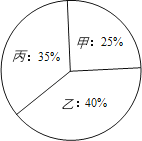
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某班去體育用品商店購買羽毛球和羽毛球拍,每只羽毛球2元,每副羽毛球拍25元.甲商店說:“羽毛球拍和羽毛球都打9折優惠”,乙商店說:“買一副羽毛球拍贈2只羽毛球”.
(1)該班如果買2副羽毛球拍和20只羽毛球,問在甲、乙兩家商店各需花多少錢?
(2)該班如果準備花90元錢全部用于買2副羽毛球拍和若干只羽毛球,請問到哪家商店購買更合算?
(3)該班如果必須買2副羽毛球拍,問當買多少只羽毛球時到兩家商店購買同樣合算?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com