
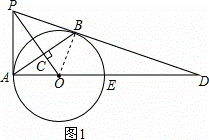
如圖,PB為⊙O的切線,B為切點,過B作OP的垂線BA,垂足為C,交⊙O于點A,連接PA、AO,并延長AO交⊙O于點E,與PB的延長線交于點D.
(1)求證:PA是⊙O的切線;
(2)若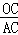 =
=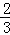 ,且OC=4,求PA的長和tanD的值.
,且OC=4,求PA的長和tanD的值.
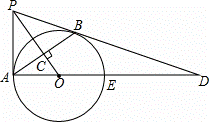
(1)證明:連接OB,則OA=OB,
∵OP⊥AB,
∴AC=BC,
∴OP是AB的垂直平分線,
∴PA=PB,
在△PAO和△PBO中,
∵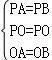 ,
,
∴△PAO≌△PBO(SSS)
∴∠PBO=∠PAO,PB=PA,
∵PB為⊙O的切線,B為切點,
∴∠PBO=90°,
∴∠PAO=90°,
即PA⊥OA,
∴PA是⊙O的切線;
(2)連接BE,

∵ =
= ,且OC=4,
,且OC=4,
∴AC=6,
∴ AB=12,
AB=12,
在Rt△ACO中,
由勾股定理得:AO= =2
=2 ,
,
∴AE=2OA=4 ,OB=OA=2
,OB=OA=2 ,
,
在Rt△APO中,
∵AC⊥OP,
∴AC2=OC•PC,
解得:PC=9,
∴OP=PC+OC=13,
在Rt△APO中,由勾股定理得:AP=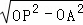 =3
=3 ,
,
∴PB=PA=3 ,
,
∵AC=BC,OA=OE,
∴OC=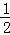 BE,OC∥BE,
BE,OC∥BE,
∴BE=2OC=8,BE∥OP,
∴△DBE∽△DPO,
∴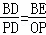 ,
,
即 ,
,
解得:BD= ,
,
在Rt△OBD中,
tanD=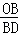 =
=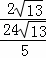 =
= .
.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
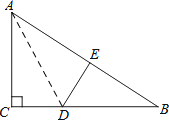
如 圖,在Rt△ABC中,∠C=90°,△ACD沿AD折疊,使得點C落在斜邊AB上的點E處.
圖,在Rt△ABC中,∠C=90°,△ACD沿AD折疊,使得點C落在斜邊AB上的點E處.
( 1)求證:△BDE∽△BAC;
1)求證:△BDE∽△BAC;
(2)已知AC=6,BC=8,求線段AD的長度.
查看答案和解析>>
科目:初中數學 來源: 題型:
如圖,一次函數的圖象與x軸、y軸分別相交于A、B兩點,且與反比例函數y=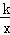 (k≠0)的圖象在第一象限交于點C,如果點B的坐標為(0,2),OA=OB,B是線段AC的中點.
(k≠0)的圖象在第一象限交于點C,如果點B的坐標為(0,2),OA=OB,B是線段AC的中點.
(1)求點A的坐標及一次函數解析式.
(2)求點C的坐標及反比例函數的解析式.
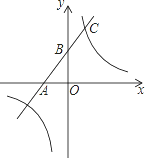
查看答案和解析>>
科目:初中數學 來源: 題型:
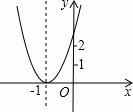
已知二次函數y=ax2+bx+c+2的圖象如圖所示,頂點為(﹣1,0),下列結論:①abc<0;②b2﹣4ac=0;③a>2;④4a﹣2b+c>0.其中正確結論的個數是( )
|
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com