
【題目】根據道路管理規定,在賀州某段筆直公路上行駛的車輛,限速40千米/時,已知交警測速點M到該公路A點的距離為10![]() 米,∠MAB=45°,∠MBA=30°(如圖所示),現有一輛汽車由A往B方向勻速行駛,測得此車從A點行駛到B點所用的時間為3秒.
米,∠MAB=45°,∠MBA=30°(如圖所示),現有一輛汽車由A往B方向勻速行駛,測得此車從A點行駛到B點所用的時間為3秒.
(1)求測速點M到該公路的距離;
(2)通過計算判斷此車是否超速.(參考數據:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.24)
≈2.24)
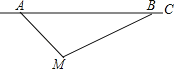
【答案】(1)10米;(2)此車沒有超速.
【解析】
試題分析:(1)過M作MN垂直于AB,在直角三角形AMN中,利用銳角三角函數定義及特殊角的三角函數值求出MN的長,即可得到結果;
(2)由三角形AMN為等腰直角三角形得到AN=MN=10米,在直角三角形BMN中,利用銳角三角函數定義求出BN的長,由AN+NB求出AB的長,根據路程除以時間得到速度,即可做出判斷.
解:(1)過M作MN⊥AB,
在Rt△AMN中,AM=10![]() ,∠MAN=45°,
,∠MAN=45°,
∴sin∠MAN=![]() ,即
,即![]() =
=![]() ,
,
解得:MN=10,
則測速點M到該公路的距離為10米;
(2)由(1)知:AN=MN=10米,
在Rt△MNB中,∠MBN=30°,
由tan∠MBN=![]() ,得:
,得:![]() =
=![]() ,
,
解得:BN=10![]() (米),
(米),
∴AB=AN+NB=10+10![]() ≈27.3(米),
≈27.3(米),
∴汽車從A到B的平均速度為27.3÷3=9.1(米/秒),
∵9.1米/秒=32.76千米/時<40千米/時,
∴此車沒有超速.


 紅果子三級測試卷系列答案
紅果子三級測試卷系列答案 課堂練加測系列答案
課堂練加測系列答案科目:初中數學 來源: 題型:
【題目】如圖,已知△ABC的面積為24,點D在線段AC上,點F在線段BC的延長線上,且BF=4CF,四邊形DCFE是平行四邊形,則圖中陰影部分的面積為( )
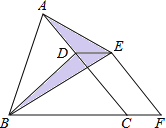
A.3 B.4 C.6 D.8
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,對稱軸為x=1的拋物線經過A(﹣1,0),B(4,5)兩點.
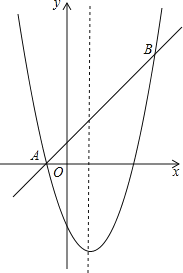
(1)求拋物線的解析式;
(2)P為直線AB上的動點,過點P作x軸的垂線交拋物線于點Q.
①當PQ=6時,求點P的坐標;
②是否存在點P,使以A、P、Q為頂點的三角形為等腰三角形?若存在,直接寫出點P的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(8分)如圖,在平面直角坐標系xOy中,一次函數y=kx+b的圖象與反比例函數y=![]() 的圖象交于A(2,3),B(-3,n)兩點.
的圖象交于A(2,3),B(-3,n)兩點.
(1)求一次函數和反比例函數的解析式;
(2)若P是y軸上一點,且滿足△PAB的面積是5,求OP的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知反比例函數![]() 和一次函數y=2x﹣1,其中一次函數的圖象經過(a,b),(a+1,b+k)兩點.
和一次函數y=2x﹣1,其中一次函數的圖象經過(a,b),(a+1,b+k)兩點.
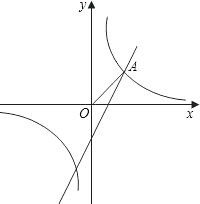
(1)求反比例函數的解析式;
(2)如圖,已知點A在第一象限,且同時在上述兩個函數的圖象上,求點A的坐標;
(3)利用(2)的結果,請問:在x軸上是否存在點P,使△AOP為等腰三角形?若存在,把符合條件的P點坐標都求出來;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如果一個正比例函數的圖象經過不同象限的兩點A(2,m),B(n,3),那么一定有( )
A.m>0,n>0 B.m>0,n<0
C.m<0,n>0 D.m<0,n<0
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com