
 的中點,連接PA,PB,PC.
的中點,連接PA,PB,PC. AP;
AP; ,求tan∠PAB的值.
,求tan∠PAB的值.
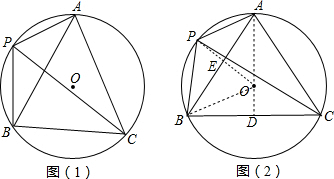
 的中點,
的中點, ∠ACB=30°,
∠ACB=30°, =tan30°=
=tan30°= ,
, PA;
PA; =
=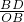 ,
, =7x,
=7x, =40x,
=40x, 的中點,
的中點, AB=20x,∠AEP=∠AEO=90°,
AB=20x,∠AEP=∠AEO=90°,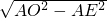 =15x,
=15x,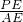 =
=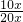 =
= ,
, .
. 的中點,則∠ACP=
的中點,則∠ACP= ∠ACB=30°,于是∠PAC=90°,然后根據30度的正切可計算出AC=
∠ACB=30°,于是∠PAC=90°,然后根據30度的正切可計算出AC= AP;
AP; =
=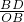 ,設OB=25x,則BD=24x,在Rt△OBD中可計算出OD=7x,再在Rt△ABD計算出AB=40x,由于點P是
,設OB=25x,則BD=24x,在Rt△OBD中可計算出OD=7x,再在Rt△ABD計算出AB=40x,由于點P是 的中點,根據垂徑定理的推論OP垂直平分AB,則AE=
的中點,根據垂徑定理的推論OP垂直平分AB,則AE= AB=20x,
AB=20x, x,所以PE=(25-4
x,所以PE=(25-4 )x,最后在Rt△APE中,利用正切的定義求解.
)x,最后在Rt△APE中,利用正切的定義求解.

 期末寶典單元檢測分類復習卷系列答案
期末寶典單元檢測分類復習卷系列答案科目:初中數學 來源: 題型:
 的坐標為(-1,0).
的坐標為(-1,0).查看答案和解析>>
科目:初中數學 來源: 題型:
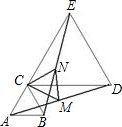 如圖,已知△ABC是等邊三角形,E是AC延長線上一點,選擇一點D,使得△CDE是等邊三角形,如果M是線段AD的中點,N是線段BE的中點,
如圖,已知△ABC是等邊三角形,E是AC延長線上一點,選擇一點D,使得△CDE是等邊三角形,如果M是線段AD的中點,N是線段BE的中點,查看答案和解析>>
科目:初中數學 來源: 題型:
 (2012•襄城區模擬)如圖,已知△ABC是等邊三角形,D、E分別在邊BC、AC上,且CD=CE,連接DE并延長至點F,使EF=AE,連接AF、BE和CF.
(2012•襄城區模擬)如圖,已知△ABC是等邊三角形,D、E分別在邊BC、AC上,且CD=CE,連接DE并延長至點F,使EF=AE,連接AF、BE和CF.查看答案和解析>>
科目:初中數學 來源: 題型:
 (2013•奉賢區二模)如圖,已知△ABC是等邊三角形,點D是BC延長線上的一個動點,以AD為邊作等邊△ADE,過點E作BC的平行線,分別交AB,AC的延長線于點F,G,聯結BE.
(2013•奉賢區二模)如圖,已知△ABC是等邊三角形,點D是BC延長線上的一個動點,以AD為邊作等邊△ADE,過點E作BC的平行線,分別交AB,AC的延長線于點F,G,聯結BE.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com