
我們容易發現:反比例函數的圖象是一個中心對稱圖形.你可以利用這一結論解決問題.
如圖,在同一直角坐標系中,正比例函數的圖象可以看作是:將![]() 軸所在的直線繞著原點
軸所在的直線繞著原點![]() 逆時針旋轉α度角后的圖形.若它與反比例函數
逆時針旋轉α度角后的圖形.若它與反比例函數![]() 的圖象分別交于第一、三象限的點
的圖象分別交于第一、三象限的點![]() 、
、![]() ,已知點
,已知點![]() 、
、![]() .
.
(1)直接判斷并填寫:不論α取何值,四邊形![]() 的形狀一定是 ;
的形狀一定是 ;
(2)①當點![]() 為
為![]() 時,四邊形
時,四邊形![]() 是矩形,試求
是矩形,試求![]() 、α、和
、α、和![]() 有值;
有值;
②觀察猜想:對①中的![]() 值,能使四邊形
值,能使四邊形![]() 為矩形的點
為矩形的點![]() 共有幾個?(不必說理)
共有幾個?(不必說理)
(3)試探究:四邊形![]() 能不能是菱形?若能, 直接寫出B點的坐標, 若不能, 說明理由.
能不能是菱形?若能, 直接寫出B點的坐標, 若不能, 說明理由.

解:(1)平行四邊形
(2)①∵點![]() 在
在![]() 的圖象上,∴
的圖象上,∴![]()
∴![]()
過![]() 作
作![]() ,則
,則![]()
在![]() 中,
中,![]()
α=30° ∴![]()
又∵點B、D是正比例函數與反比例函數圖象的交點,
∴點B、D關于原點O成中心對稱
∴OB=OD=![]()
∵四邊形![]() 為矩形,且
為矩形,且![]()
![]()
∴![]() ∴
∴![]() ;
;
②能使四邊形![]() 為矩形的點B共有2個;
為矩形的點B共有2個;
(3)四邊形![]() 不能是菱形.
不能是菱形.
法一:∵點![]() 、
、![]() 的坐標分別為
的坐標分別為![]() 、
、![]()
∴四邊形![]() 的對角線
的對角線![]() 在
在![]() 軸上.
軸上.
又∵點![]() 、
、![]() 分別是正比例函數與反比例函數在第一、三象限的交點.
分別是正比例函數與反比例函數在第一、三象限的交點.
∴對角線![]() 與
與![]() 不可能垂直.
不可能垂直.
∴四邊形![]() 不能是菱形
不能是菱形
法二:若四邊形ABCD為菱形,則對角線AC⊥BD,且AC與BD互相平分,
因為點A、C的坐標分別為(-m,0)、(m,0)
所以點A、C關于原點O對稱,且AC在x軸上.
所以BD應在y軸上,這與“點B、D分別在第一、三象限”矛盾,
所以四邊形ABCD不可能為菱形.


科目:初中數學 來源: 題型:
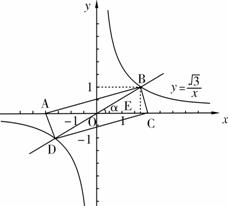
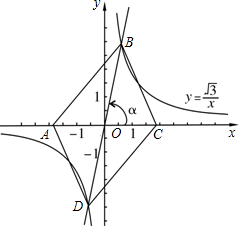 我們容易發現:反比例函數的圖象是一個中心對稱圖形.你可以利用這一結論解決問題.如圖,在同一直角坐標系中,正比例函數的圖象可以看作是:將x軸所在的直線繞著原點O逆時針旋轉α度角后的圖形.若它與反比例函數y=
我們容易發現:反比例函數的圖象是一個中心對稱圖形.你可以利用這一結論解決問題.如圖,在同一直角坐標系中,正比例函數的圖象可以看作是:將x軸所在的直線繞著原點O逆時針旋轉α度角后的圖形.若它與反比例函數y=
| ||
| x |
查看答案和解析>>
科目:初中數學 來源: 題型:
 我們容易發現:反比例函數的圖象是一個中心對稱圖形.你可以利用這一結論解決問題.如圖,在同一直角坐標系中,正比例函數的圖象可以看作是:將x軸所在的直線繞著原點O逆時針旋轉α度角后的圖形.若它與反比例函數y=
我們容易發現:反比例函數的圖象是一個中心對稱圖形.你可以利用這一結論解決問題.如圖,在同一直角坐標系中,正比例函數的圖象可以看作是:將x軸所在的直線繞著原點O逆時針旋轉α度角后的圖形.若它與反比例函數y=| 1 | x |
查看答案和解析>>
科目:初中數學 來源:2013屆江西省吉安朝宗實驗學校九年級第一次段考數學試卷(帶解析) 題型:解答題
我們容易發現:反比例函數的圖象是一個中心對稱圖形,你可以利用這一結論解決問題。如圖,在同一直角坐標系中,正比例函數的圖象可以看作是將x軸所在的直線繞著原點O逆時針旋轉 度后的圖形。它與反比例函數
度后的圖形。它與反比例函數 的圖象分別交于第一、三象限的點B、D,已知點A(-m,0)、C(m,0)。
的圖象分別交于第一、三象限的點B、D,已知點A(-m,0)、C(m,0)。
(1)判斷并填寫,不論 取何值,四邊形ABCD的形狀一定是______;
取何值,四邊形ABCD的形狀一定是______;
(2)①當點B坐標為(p,1)時,四邊形ABCD是矩形,試求p、 和m的值;
和m的值;
②觀察猜想:對①中的m值,能使四邊形ABCD為矩形的點B共有幾個?(不必說理)
(3)試探究:四邊形ABCD能不能是菱形?若能,直接寫出B點的坐標;若不能,說明理由。
查看答案和解析>>
科目:初中數學 來源:2012-2013學年江西省九年級第一次段考數學試卷(解析版) 題型:解答題
我們容易發現:反比例函數的圖象是一個中心對稱圖形,你可以利用這一結論解決問題。如圖,在同一直角坐標系中,正比例函數的圖象可以看作是將x軸所在的直線繞著原點O逆時針旋轉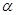 度后的圖形。它與反比例函數
度后的圖形。它與反比例函數 的圖象分別交于第一、三象限的點B、D,已知點A(-m,0)、C(m,0)。
的圖象分別交于第一、三象限的點B、D,已知點A(-m,0)、C(m,0)。

(1)判斷并填寫,不論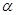 取何值,四邊形ABCD的形狀一定是______;
取何值,四邊形ABCD的形狀一定是______;
(2)①當點B坐標為(p,1)時,四邊形ABCD是矩形,試求p、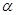 和m的值;
和m的值;
②觀察猜想:對①中的m值,能使四邊形ABCD為矩形的點B共有幾個?(不必說理)
(3)試探究:四邊形ABCD能不能是菱形?若能,直接寫出B點的坐標;若不能,說明理由。
查看答案和解析>>
科目:初中數學 來源:福建省中考真題 題型:解答題
 的圖象分別交于第一、三象限的點B,D,已知點A(-m,0)、C(m,0)。
的圖象分別交于第一、三象限的點B,D,已知點A(-m,0)、C(m,0)。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com