
【題目】![]() 是等腰直角三角形,點
是等腰直角三角形,點![]() 為線段
為線段![]() 上一點(
上一點(![]() 點不和
點不和![]() 兩點重合),連接
兩點重合),連接![]() 并延長
并延長![]() ,在
,在![]() 的延長線上找一點
的延長線上找一點![]() ,使
,使![]() .點
.點![]() 為線段
為線段![]() 上一點(
上一點(![]() 點不和
點不和![]() 兩點重合),連接
兩點重合),連接![]() ,交
,交![]() 于點
于點![]() .
.
(1)如圖1,若![]() 是線段
是線段![]() 的中點,求
的中點,求![]() .
.
(2)如圖2,若點![]() 是線段
是線段![]() 的中點,
的中點,![]() ,求證:
,求證:![]() .
.

【答案】(1)![]() ;(2)見解析
;(2)見解析
【解析】
(1)根據(jù)等腰直角三角形的性質得到![]() ,根據(jù)勾股定理得到
,根據(jù)勾股定理得到![]() 根據(jù)線段的中點的定義得到
根據(jù)線段的中點的定義得到![]() ,由勾股定理得到結論;
,由勾股定理得到結論;
(2)過A作AH∥CD交BD于H,得到∠AHD=∠CDH,根據(jù)全等三角形的性質得到DE=EH,AH=CD,推出四邊形AHCD是矩形,得到∠HAD=90°,根據(jù)全等三角形的性質得到BH=CF,由線段的和差得到結論.
解:(1)∵△ABC是等腰直角三角形,![]()
![]()
∵AD⊥CD,
∴∠ADC=90°,
∵CD=1,
∴![]()
∵F是線段AD的中點,
∴![]()
![]()
(2)過A作AH∥CD交BD于H,
∴∠AHD=∠CDH,
∵點E是線段AC中點,
∴AE=CE,
在△AEH與△CED中,
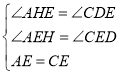
∴△AEH≌△CED(AAS),
∴DE=EH,AE=CE,
∴四邊形AHCD是平行四邊形,
∵∠ADC=90°,
∴四邊形AHCD是矩形,
∴∠HAD=90°,
∵∠BAC=90°,
∴∠BAH=∠FAC,
∵DE⊥CF,
∴∠DFG=∠CDG,
∴∠AHE=∠DFG,
∴∠AHB=∠AFC,
在△ABH與△ACF中
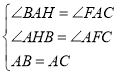
∴△ABH≌△ACF(AAS),
∴BH=CF,
∵BE=BH+EH,
∴CF+DE=BE.



 開心快樂假期作業(yè)暑假作業(yè)西安出版社系列答案
開心快樂假期作業(yè)暑假作業(yè)西安出版社系列答案 名題訓練系列答案
名題訓練系列答案科目:初中數(shù)學 來源: 題型:
【題目】某商店第一次用3000元購進某款書包,很快賣完,第二次又用2400元購進該款書包,但這次每個書包的進價是第一次進價的1.2倍,數(shù)量比第一次少了20個.
(1)求第一次每個書包的進價是多少元?
(2)若第二次進貨后按80元/個的價格銷售,恰好銷售完一半時,根據(jù)市場情況,商店決定對剩余的書包按同一標準一次性打折銷售,但要求這次的利潤不少于480元,問最低可打幾折?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】一家用電器開發(fā)公司研制出一種新型電子產品,每件的生產成本為![]() 元,按定價
元,按定價![]() 元出售,每月可銷售
元出售,每月可銷售![]() 萬件.為了增加銷量,公司決定采取降價的辦法,經市場調研,每降價
萬件.為了增加銷量,公司決定采取降價的辦法,經市場調研,每降價![]() 元,月銷售量可增加
元,月銷售量可增加![]() 萬件.
萬件.
(1)求出月銷售量![]() (萬件)與銷售單價
(萬件)與銷售單價![]() (元)之間的函數(shù)關系式(不必寫
(元)之間的函數(shù)關系式(不必寫![]() 的取值范圍);
的取值范圍);
(2)求出月銷售利潤![]() (萬元)(利潤
(萬元)(利潤![]() 售價-成本價)與銷售單價
售價-成本價)與銷售單價![]() (元)之間的函數(shù)關系式(不必寫
(元)之間的函數(shù)關系式(不必寫![]() 的取值范圍);
的取值范圍);
(3)請你通過(2)中的函數(shù)關系式及其大致圖象幫助公司確定產品的銷售單價范圍,使月銷售利潤不低于![]() 萬元.
萬元.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】我們知道不等式的兩邊加(或減)同一個數(shù)(或式子),不等號的方向不變.不等式組是否也具有類似的性質呢?請解答下列問題.
(1)完成下列填空:
已知 | 用“<”或“>”填空 |
| 5+2_____3+1 |
| ﹣3﹣1_____﹣5﹣2 |
| 1﹣2_____4+1 |
(2)一般地,如果![]() 那么a+c_____b+d(用“<”或“>”填空).請你說明上述性質的正確性.
那么a+c_____b+d(用“<”或“>”填空).請你說明上述性質的正確性.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,正方形ABDE、CDFI、EFGH的面積分別為25、9、16,△AEH、△BDC、△GFI的面積分別為S1、S2、S3,則S1+S2+S3=_____.
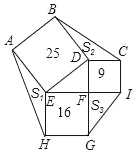
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖所示,梯形ABCD中,AB∥DC,∠B=90°,AD=15,AB=16,BC=12,點E是邊AB上的動點,點F是射線CD上一點,射線ED和射線AF交于點G,且∠AGE=∠DAB.
(1)求線段CD的長;
(2)如果△AEG是以EG為腰的等腰三角形,求線段AE的長;
(3)如果點F在邊CD上(不與點C、D重合),設AE=x,DF=y,求y關于x的函數(shù)解析式,并寫出x的取值范圍.
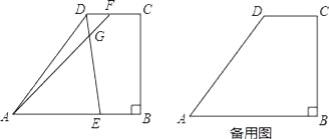
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,DB∥AC,且DB=![]() AC,E是AC的中點,
AC,E是AC的中點,
(1)求證:BC=DE;
(2)連接AD、BE,若要使四邊形DBEA是矩形,則給△ABC添加什么條件,為什么?

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在平面直角坐標中,反比例函數(shù)y=![]() (x>0)的圖象經過點A(1,4),B(a,b),其中a>1.過點A作x軸垂線,垂足為C,過點B作y軸垂線,垂足為D,AC與BD交于點E,連接AD,DC,CB.
(x>0)的圖象經過點A(1,4),B(a,b),其中a>1.過點A作x軸垂線,垂足為C,過點B作y軸垂線,垂足為D,AC與BD交于點E,連接AD,DC,CB.
(1)求k的值;
(2)求證:DC∥AB;
(3)當AD∥BC時,求直線AB的函數(shù)表達式.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】下列游戲對雙方公平的是( )
A. 隨意轉動被等分成![]() 個扇形,且分別均勻涂有紅、黃、綠三種顏色的轉盤,若指針指向綠色區(qū)域,則小明勝,否則小亮勝
個扇形,且分別均勻涂有紅、黃、綠三種顏色的轉盤,若指針指向綠色區(qū)域,則小明勝,否則小亮勝
B. 從一個裝有![]() 個紅球,
個紅球,![]() 個黃球和
個黃球和![]() 個黑球(這些球除顏色外完全相同)的袋中任意摸出一個球,若是紅球,則小明勝,否則小亮勝
個黑球(這些球除顏色外完全相同)的袋中任意摸出一個球,若是紅球,則小明勝,否則小亮勝
C. 投擲一枚均勻的正方體形狀的骰子,若偶數(shù)點朝上,則小明勝,若是奇數(shù)點朝上,則小亮勝
D. 從分別標有數(shù)![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的五張紙條中,任意抽取一張,若抽到的紙條所標的數(shù)字為偶數(shù),則小明勝,若抽到的紙條所標的數(shù)字為奇數(shù),則小亮勝
的五張紙條中,任意抽取一張,若抽到的紙條所標的數(shù)字為偶數(shù),則小明勝,若抽到的紙條所標的數(shù)字為奇數(shù),則小亮勝
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com